Gesetze des
Skalarproduktes |
 Kommutativgesetz Kommutativgesetz
Das Skalarprodukt ist
kommutativ, d.h. es gilt:
 · · = =  · ·
|
 Distributivgesetz Distributivgesetz
Das Skalarprodukt ist
distributiv, d.h. es gilt:
k·( + + ) =
k· ) =
k· + k· + k· k = reelle Zahl
k = reelle Zahl
|
 Gemischtes Assoziativgesetz Gemischtes Assoziativgesetz
Das Skalarprodukt ist in
Verbindung mit reellen Zahlen
assoziativ:
(k· )· )· = k·( = k·( · · )
k = reelle Zahl )
k = reelle Zahl
 ·(k· ·(k· ) = k·( ) = k·( · · )
k = reelle Zahl )
k = reelle Zahl
|
 Anmerkung zum Assoziativgesetz Anmerkung zum Assoziativgesetz
Da es ein gemischtes Assoziativgesetz gibt, stellt sich
automatisch die Frage, ob es auch ein "ungemischtes"
Assoziativgesetz gibt, d.h. ob gilt: ( · · )· )·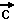 = = ·( ·( · ·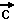 )? )?
Dieses Gesetz gilt nicht:
Wir betrachten die linke Seite der Gleichung: ( · · ) ist eine ) ist eine
reelle Zahl, also ist ( · · )· )·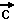 ein zu ein zu 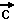 paralleler Vektor. paralleler Vektor.
Dagegen ist die rechte Seite der Gleichung, also  ·( ·( · ·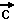 ), ),
ein zu  paralleler Vektor. Das Skalarprodukt ist also paralleler Vektor. Das Skalarprodukt ist also
in der Regel nicht assoziativ.
|