Beweis: Nun wollen wir die Formel von der vorigen Seite beweisen. Sie lautete:
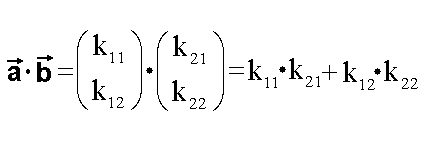Zuerst wechseln wir die Schreibweise. Statt in Koordinatenform schreiben wir das Skalarprodukt in Komponentenform:
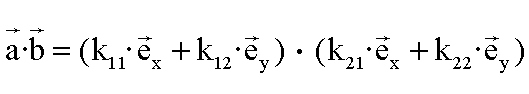Da das Skalarprodukt distributiv ist, können wir die
Klammern ausmultiplizieren:
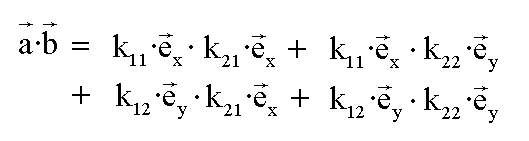Da das Skalarprodukt orthogonaler Vektoren gleich 0 ist,
vereinfacht sich die Formel zu:
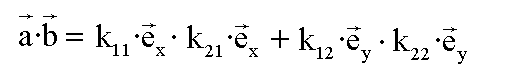Nun fassen wir zusammen:
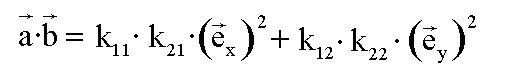Die Quadrate von Einheitsvektoren haben den Wert 1,
und somit erhalten wir die gewünschte Formel:
Beweis:
Zuerst wechseln wir die Schreibweise. Statt in Koordinatenform
Da das Skalarprodukt distributiv ist, können wir die
Klammern ausmultiplizieren:
Da das Skalarprodukt orthogonaler Vektoren gleich 0 ist,
vereinfacht sich die Formel zu:
Nun fassen wir zusammen:
Die Quadrate von Einheitsvektoren haben den Wert 1,
und somit erhalten wir die gewünschte Formel:
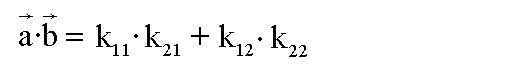
