Definition
der
Stetigkeit |
|
Gegeben sei eine Funktion f, die Stelle x0
auf der x-Achse
und der zuzugehörigen Funktionswert f(x0) auf der y-Achse.

Nun wählen wir eine (beliebig kleine) Umgebung U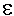 mit einer
Breite mit einer
Breite
von 2·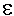 , deren
Elemente zwischen f(x0)- , deren
Elemente zwischen f(x0)-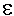 und f(x0)+ und f(x0)+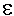 liegen : liegen :

Dann ist
die Funktion f an der Stelle x0 stetig, wenn 2 Dinge gelten:
 Es gibt auf der
x-Achse eine Umgebung U Es gibt auf der
x-Achse eine Umgebung U die klein genug ist, die klein genug ist,
sodaß ihre Funktionswerte (bilden den Wertebereich W) alle
innerhalb dieser Umgebung U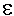 liegen liegen  Zu jeder anderen (kleineren) Zu jeder anderen (kleineren)
Umgebung U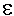 existiert ebenfalls eine passende
Umgebung U
existiert ebenfalls eine passende
Umgebung U : :

Die Definition der Stetigkeit lautet also:
Zu jeder Umgebung U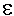 existiert mindestens eine
Umgebung U existiert mindestens eine
Umgebung U , ,
sodaß alle Funktionswerte von U (Wertebereich) in U (Wertebereich) in U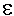 liegen: liegen:
 |
|
|