Stetigkeit
der
Wurzelfunktion
(für alle x0>0)
Seite 2/2 |
|
Der Wert des Bruches ändert sich nicht, wenn
wir die
Betragsstriche um den gesamten Bruch schreiben, anstatt
einzeln um Zähler und um den Nenner:

Der Zähler kann als 3.Binom interpretiert werden:

Nun können wir kürzen:

Weil Wurzeln immer positiv sind, sind die
Betragstriche überflüssig:

Auf der vorigen Seite haben wir erläutert, daß wir
beweisen
müssen, daß es zu jedem 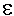 >0 mindestens ein >0 mindestens ein  >0 gibt, >0 gibt,
sodaß die "Behauptung" und somit die Ungleichung  wahr wird. wahr wird.
Weil wir nur die Existenz von  -Werten beweisen müssen, -Werten beweisen müssen,
dürfen wir den Wert  kleiner als nötig berechnen. Dazu streichen kleiner als nötig berechnen. Dazu streichen
wir die "Wurzel aus x" aus der Ungleichung:

Nun haben wir eine Ungleichung für  , in der , in der  nur noch von nur noch von
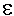 und x0
abhängt. Mit dieser Ungleichung kann man zu jeder und x0
abhängt. Mit dieser Ungleichung kann man zu jeder
(beliebig kleinen) 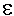 -Umgebung um f(x0) ein passendes -Umgebung um f(x0) ein passendes  >0 >0
angeben, und damit ist die Funktion stetig.
|
|