Version: 1.1 |
Inhalt zu: Trigonometrie I ZURÜCK |
||||||||||||||||||||||
| Info-Seite | Vorkenntnisse: ... Themen: ... Infos: www.mathematik.net | ||||||||||||||||||||||
| Bezeichnungen im rechtwinkligen Dreieck |
 |
||||||||||||||||||||||
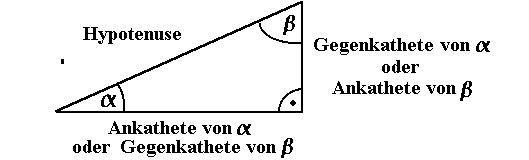| Satz des Pythagoras |
Im rechtwinkligen Dreieck gilt: a²
+ b² = c² (wenn c die Hypotenuse ist) Anwendung: Sind zwei Seiten bekannt, so kann man die dritte berechnen. |
||||||||||||||||||||||
| Winkelsumme | Winkelsummensatz: Die Summe der Innenwinkel im Dreieck ist 180°. | ||||||||||||||||||||||
| Ähnliche Dreiecke |
Sind zwei Dreiecke in allen drei Winkeln gleich, so nennt man sie ähnlich. Wegen dem Winkelsummensatz genügen auch schon zwei Winkel. |
||||||||||||||||||||||
| Was ist ein Seitenverhältnis |
In jedem Dreieck gibt es 6 Seitenverhältnisse. Ist das Dreieck rechtwinklig, so haben sie Namen wie z.B.: Gegenkathete von  / Hypotenuse |
||||||||||||||||||||||
| Bei ähnlichen Dreiecken gilt: Seitenverhältnis von der Größe des Dreiecks unabhängig. |
Ähnliche
Dreiecke haben gleiche Seitenverhältnisse: a1/c1= a2/c2=a3/c3 |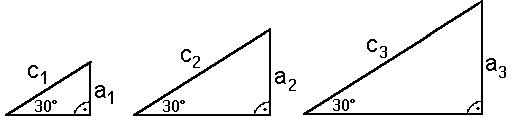
||||||||||||||||||||||
| Die Seiten- verhältnisse im Dreieck sind winkelabhängig |
Die
Seitenverhältnisse (hier: a/c) sind nur winkelabhängig (hier: von 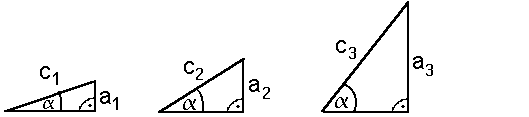): Das Seitenverhältnis a/c (Gegenkathete von /Hypotenuse)
heißt Sinus . |
||||||||||||||||||||||
| Tabellen für die Seitenverhältnisse: Die Sinustabelle |
Die Mathematiker merken sich das "winkelabhängige" Seitenverhältnis "Gegenkathete von / Hypotenuse" in einer sogenannten Sinustabelle:
|
||||||||||||||||||||||
| 1.Anwendung der Sinustabelle: Seitenberechnung |
Mit der
Sinus-Tabelle kann man alle Seiten eines rechtwinkligen Dreiecks berechenen, auch wenn nur eine Seite bekannt ist (und die Winkel):  |
||||||||||||||||||||||
| Variante | Eine kleine Variante dieser Aufgabe: Die Hypotenuse ist gesucht. | ||||||||||||||||||||||
| 2.Anwendung der Sinustabelle: |
Umgekehrt
kann man mit der Sinustabelle auch die Winkel berechnen, wenn zwei der drei Seiten bekannt sind. Ein Beispiel ... |