Version: 1.1
©Raddy '99

Trigonometrie I                                                ZURÜCK

Die längste Seite im rechwinkligen Dreieck liegt dem     rechten Winkel gegenüber und wird Hypotenuse genannt. Die beiden übrigen Seiten werden Katheten genannt.

Beispiel
      Gegeben sei das folgende Dreieck:
     
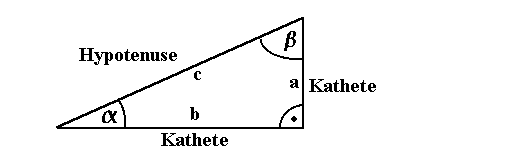
      Dann ist die Seite c die Hypotenuse, weil sie dem rechten
      Winkel gegenüberliegt. Die beiden übrigen Seiten nennt man
      Katheten. Im Beispiel sind dies die Seiten a und b.

Gegenkathete und Ankathete
      Die Katheten werden nochmals unterschieden:

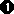Die Kathete, die dem Winkel gegenüber liegt, nennt man     die Gegenkathete von . Die Kathete, die am Winkel anliegt, nennt man die      Ankathete von .

Beispiel
      Gegeben sei wieder das gleiche Dreieck wie oben:

      

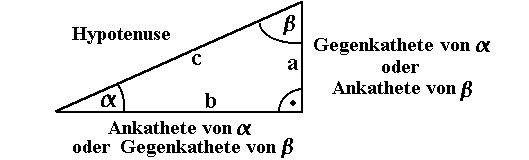
       Zuerst betrachten wir die Seite a:
       Da die Seite a dem Winkel gegenüberliegt, ist die Seite a die
       Gegenkathete des Winkels  . Das die Seite a aber auch am
       Winkel 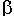anliegt, ist sie gleichzeitig die Ankathete von .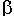

       Nun zur Seite b:
       Da die Seite b dem Winkel 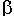gegenüberliegt, ist die Seite b die
       Gegenkathete des Winkels 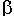 . Das die Seite b aber auch am
       Winkel anliegt, ist sie gleichzeitig die Ankathete von .