Vorbemerkung
Auf der Vorseite haben wir "ähnliche" Dreiecke" kennengelernt.
Ähnliche Dreiecke haben eine wichtige Eigenschaft:
Satz
Zwei "ähnliche Dreiecke"
haben gleiche Seitenverhältnisse.
Erklärung des Satzes
Zuerst zeichnen wir zwei ähnliche Dreiecke, also zwei Dreiecke
mit gleichen Winkeln. Im Beispiel zeichen wir
zwei 30°/90°/60° Dreiecke:
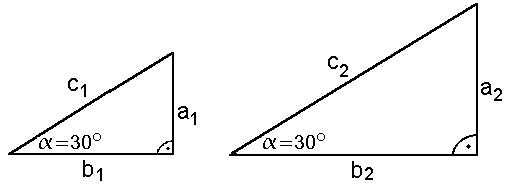Exemplarisch überprüfen wir eines der sechs möglichen Seiten-
verhältnisse, z.B. das Verhältnis Gegenkathete / Hypotenuse.
Im Beispiel entspricht dies dem Verhältnis a/c:
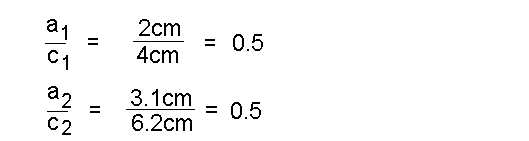Man sieht: Bei den beiden zueinander ähnlichen Dreiecken ist
das Seitenverhältnis "Gegenkathete / Hypotenuse" konstant.
Der Satz sagt weiter, daß auch die anderen Seitenverhältnisse
konstant sind:
Ankathete von / Hypotenuse (im Bild: b/c)
Gegenkathete von / Ankathete von (im Bild: a/b)
Ankathete von / Gegenkathete von (im Bild: b/a)
Aus Platzmangel verzichten wir jedoch darauf, dies zu demonstrieren.
Als Übung kann man aber mit einem Lineal nachmessen.
Vorbemerkung
Auf der Vorseite haben wir "ähnliche" Dreiecke" kennengelernt.
Ähnliche Dreiecke haben eine wichtige Eigenschaft:
Exemplarisch überprüfen wir eines der sechs möglichen Seiten-
verhältnisse, z.B. das Verhältnis Gegenkathete 
Man sieht: Bei den beiden zueinander ähnlichen Dreiecken ist
das Seitenverhältnis "Gegenkathete