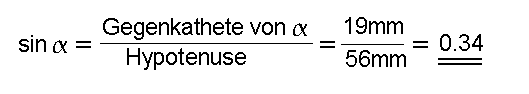| Sinus-Tabelle |
 Vorbemerkung Vorbemerkung
Auf der
Vorseite haben wir gesehen, daß das Seitenverhältnis
Sinus  (Gegenkathete von (Gegenkathete von  / Hypotenuse) vom Winkel / Hypotenuse) vom Winkel  abhängt. abhängt.
Genauer gesagt: Zu jedem Seitenverhältnis "Sinus  "
gehört genau "
gehört genau
ein Winkel  und umgekehrt: Zu jedem Winkel und umgekehrt: Zu jedem Winkel  gehört
genau ein gehört
genau ein
Seitenverhältnis "Sinus  ". ".
Formal gesagt: Das Seitenverhältnis "Sinus  " und
der Winkel " und
der Winkel 
(mit: 0°< <90°) bilden eine bijektive Funktion. <90°) bilden eine bijektive Funktion.
Die Mathematiker merken sich nun in einer Tabelle, zu
welchen
welchem Winkel welches Seitenverhältnis gehört.
 Die Sinus-Tabelle Die Sinus-Tabelle
Das
folgende Bild zeigt eine Sinus-Tabelle:
 |
0° |
10° |
20° |
30° |
40° |
50° |
60° |
70° |
80° |
90° |
Gegenkathete
Hypotenuse |
0 |
0.17 |
0.34 |
0.50 |
0.64 |
0.77 |
0.87 |
0.94 |
0.98 |
1 |
Nun wollen wir zeigen, wie solch eine Sinus-Tabelle entsteht.
Exemplarisch zeigen wir, wie der Sinus von 20°
ermittelt wird:
1. Man zeichnet ein
rechwinkliges Dreieck, mit einem 20° Winkel:
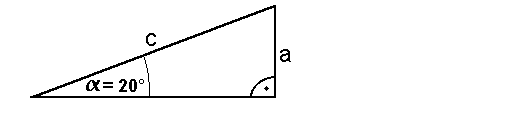
2. Nun mißt man die Seiten a
und c:
a= 19mm
c=56mm
3. Man teilt die Seite a
durch die Seite c, also die
Gegenkathete von  durch die Hypotenuse, und durch die Hypotenuse, und
erhält den Sinus von 20°:
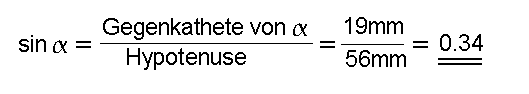
 Übung Übung
Man ermittle
am folgenden 10°/90°/80° Dreieck den Sinus von 10°:
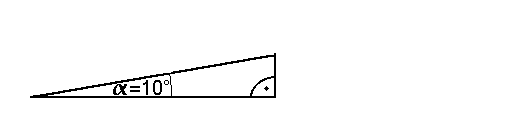
Lösung: Die Gegenkathete von  beträgt
9mm, die Hypotenuse beträgt
9mm, die Hypotenuse
beträgt 53mm. Der Sinus  beträgt 9mm/53mm = 0.17 beträgt 9mm/53mm = 0.17 |