1.Anwendung
der Sinustabelle:
Seitenberechnung
|
 Worum geht's
Auf der vorigen Seite haben wir in einer Tabelle zu einigen
Winkeln Worum geht's
Auf der vorigen Seite haben wir in einer Tabelle zu einigen
Winkeln  den dazugehörigen Sinus den dazugehörigen Sinus  angegeben, also das
Verhältnis Gegenkathete von angegeben, also das
Verhältnis Gegenkathete von  zur Hypotenuse. zur Hypotenuse.
 |
0° |
10° |
20° |
30° |
40° |
50° |
60° |
70° |
80° |
90° |
Gegenkathete
Hypotenuse |
0 |
0.17 |
0.34 |
0.50 |
0.64 |
0.77 |
0.87 |
0.94 |
0.98 |
1 |
Nun wollen wir zeigen, wozu man diese Tabelle gebrauchen kann.
Wir werden auf den nächsten Seiten zeigen, daß man mit einer Sinus-
tabelle die Seiten eines rechtwinkligen Dreiecks berechnen kann,
auch wenn nur eine Seite des Dreiecks und einer der beiden spitzen
Winkel bekannt ist (Spitzer Winkel = Ein Winkel kleiner als 90°).
 Seitenberechung am rechtwinkligen Dreieck
Als Einführung wollen wir mit Hilfe der Sinus-Tabelle die Seite a im
folgenden rechtwinkligen Dreieck berechnen, in dem die Seite c und
der Winkel Seitenberechung am rechtwinkligen Dreieck
Als Einführung wollen wir mit Hilfe der Sinus-Tabelle die Seite a im
folgenden rechtwinkligen Dreieck berechnen, in dem die Seite c und
der Winkel  bekannt sind: bekannt sind:
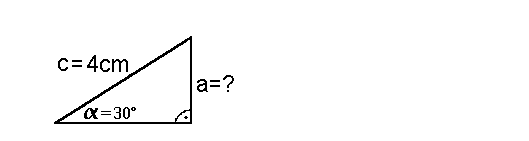 Man bildet dazu den Sinus
Man bildet dazu den Sinus  , also das Seitenverhältnis Gegenkathete
von , also das Seitenverhältnis Gegenkathete
von  zur Hypotenuse: zur Hypotenuse:
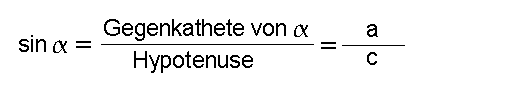 Diese Formel stellt man nach der unbekannten Seite a um, und setzt
die gegebenen Werte ein (wobei sin30° durch die Tabelle gegeben ist).
Diese Formel stellt man nach der unbekannten Seite a um, und setzt
die gegebenen Werte ein (wobei sin30° durch die Tabelle gegeben ist).
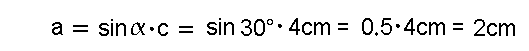 Lösung: Die Seite a ist somit 2cm lang.
Lösung: Die Seite a ist somit 2cm lang.
 Anmerkung: Pythagoras contra Sinustabelle
Wir haben soeben mit der Sinustabelle zur Seitenberechnung benutzt.
In diesem Zusammenhang erinnern wir uns, daß man auch mit dem Satz
des Pythagoras die Seiten eines rechtwinkligen Dreiecks berechnen
kann.
Beim Satz des Pythagoras müssen aber zwei Seiten bekannt sein,
um die dritte zu berechnen. Andererseites hat der Satz des Pythagoras
den Vorteil, daß keiner der spitzen Winkel bekannt sein muß.
Weitere Aufgaben am Ende von "Trigonometrie II" Anmerkung: Pythagoras contra Sinustabelle
Wir haben soeben mit der Sinustabelle zur Seitenberechnung benutzt.
In diesem Zusammenhang erinnern wir uns, daß man auch mit dem Satz
des Pythagoras die Seiten eines rechtwinkligen Dreiecks berechnen
kann.
Beim Satz des Pythagoras müssen aber zwei Seiten bekannt sein,
um die dritte zu berechnen. Andererseites hat der Satz des Pythagoras
den Vorteil, daß keiner der spitzen Winkel bekannt sein muß.
Weitere Aufgaben am Ende von "Trigonometrie II"
|
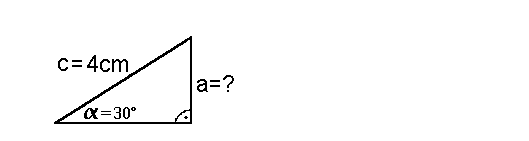 Man bildet dazu den Sinus
Man bildet dazu den Sinus 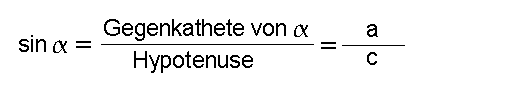 Diese Formel stellt man nach der unbekannten Seite a um, und setzt
die gegebenen Werte ein (wobei sin30° durch die Tabelle gegeben ist).
Diese Formel stellt man nach der unbekannten Seite a um, und setzt
die gegebenen Werte ein (wobei sin30° durch die Tabelle gegeben ist).
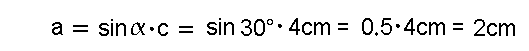 Lösung: Die Seite a ist somit 2cm lang.
Lösung: Die Seite a ist somit 2cm lang.