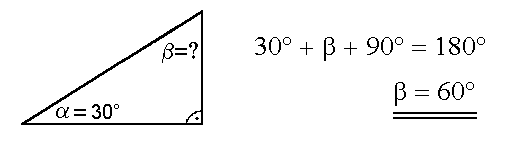Version: 1.1
©Raddy '99

Trigonometrie I                                         ZURÜCK
2.Anwendung der Sinustabelle:
Winkelberechnung		 a-absatz.pcx (280 Byte)Rückblick
      Im vorigen Kapitel haben wir mit der Sinustabelle aus einer Seite
      (Hypotenuse) und einem Winkel (a-g-alpa.pcx (200 Byte)) eine weitere Seite
      (Gegenkathete von 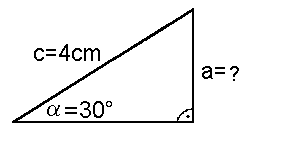a-g-alpa.pcx (200 Byte)) berechnet:
      tr2s2p1.pcx (2078 Byte)

a-absatz.pcx (280 Byte)Winkelberechnung
      Sind umgekehrt zwei Seiten gegeben (im Bild unten: die Gegen-
      kathete zu a-g-alpa.pcx (200 Byte) und die Hypotenuse), so können wir, ebenfalls mit der
      Sinustabelle, die Winkel des Dreiecks berechnen. Dazu ein Beispiel: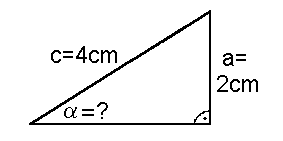

a-absatz.pcx (280 Byte)Beispiel
      tr2s0p4.pcx (3185 Byte)
Zuerst bilden wir das Seitenverhältnis
Sinus a-g-alpa.pcx (200 Byte), also das Seitenverhältnis
Gegenkathete von 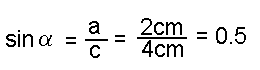a-g-alpa.pcx (200 Byte) zur Hypotenuse:
tr2s2p3.pcx (312 Byte)

      Nun schauen wir in der Sinustabelle nach, bei welchem Winkel der
      Sinus den Wert 0.5 hat. Es ist der Winkel a-g-alpa.pcx (200 Byte) = 30°:

           a-g-alpa.pcx (200 Byte) 0° 10° 20° 30° 40° 50° 60° 70° 80° 90°
Gegenkathete
Hypotenuse

   0

 0.17 0.34 0.50 0.64 0.77 0.87 0.94 0.98 1

      Nun müssen wir noch den Winkel a-g-beta.pcx (215 Byte) berechnen. Dies geschieht mit
      dem Winkelsummensatz:
      tr2s2p4.pcx (3008 Byte)

 

 

© mathematik.net