Version: Test
©Raddy '99

Inhalt zu: Trigonometrie II              ZURÜCK
Info-Seite Vorkenntnisse: ...      Themen:   ...     Infos: www.mathematik.net
Cosinus Im vorigen Kapitel (Trigonometrie I) definierten wir das Seitenverhältnis
Gegenkathete von 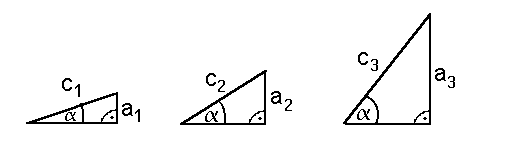a-g-alpa.pcx (200 Byte) zur Hypothenuse als den Sinus von a-g-alpa.pcx (200 Byte) (im Bild: a/c):
tr1s0p2.pcx (3922 Byte)
Nun zum Seitenverhältnis Ankathete von a-g-alpa.pcx (200 Byte) / Hypothenuse (Bild: b/c).
Diese Seitenverhältnis nennt man den Cosinus von a-g-alpa.pcx (200 Byte). Auch der Cosinus
ist vom Winkel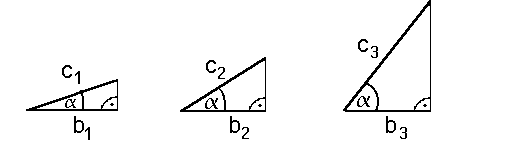a-g-alpa.pcx (200 Byte) abhängig, und von der Größe des Dreiecks unabhängig:
tr2s0p3.pcx (3244 Byte)
     a-g-alpa.pcx (200 Byte) 0° 10° 20° 30° 40° 50° 60° 70° 80° 90°

  Ankathete 
Hypothenuse

 1 0,98 0,94 0,87 0,77 0,64 0,5 0,34 0,17 0
Tangens Neben Sinus und Cosinus gibt es noch ein drittes Seitenverhältnis:
Das Seitenverhältnis "Gegenkathete von a-g-alpa.pcx (200 Byte) zur Ankathete von a-g-alpa.pcx (200 Byte)"
(Bild: a/b), genannt: Tangens 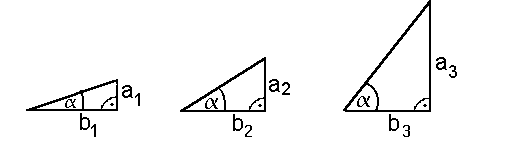a-g-alpa.pcx (200 Byte). Auch dieses Seitenverhältnis ist vom
Winkela-g-alpa.pcx (200 Byte) abhängig, und von der Größe des Dreieck unabhängig:
tr2s0p4.pcx (3199 Byte)
     a-g-alpa.pcx (200 Byte) 0° 10° 20° 30° 40° 50° 60° 70° 80° 90°
Gegenkathete
  Ankathete		 0 0,18 0,36 0,58 0,84 1,19 1,73 2,74 5,67 ---
Cotangens Das Seitenverhältnis Ankathete von  a-g-alpa.pcx (200 Byte)  zur Gegenkathete von  a-g-alpa.pcx (200 Byte)
nennt man Cotangens.
Der Cotangens ist der Kehrwert des Tangens: cot a-g-alpa.pcx (200 Byte) = tan 1/a-g-alpa.pcx (200 Byte)
Aufgabentypen Es gibt 9 Aufgabentypen beim Berechnen rechtwinkliger Dreiecke.

 
Übungen Übungen zur Berechnung rechtwinkliger Dreiecke