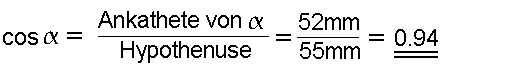Version: Test
©Raddy '99

Trigonometrie II                                             ZURÜCK
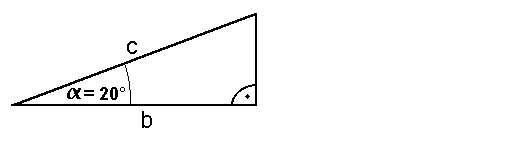
Der Cosinus a-absatz.pcx (280 Byte)Rückblick
      Bis jetzt haben wir das Seitenverhältnis Gegenkathete zur Hypothenuse
      (im Bild a/c) kennengelernt, und dieses Seitenverhältnis Sinus genannt.
      Wir stellten fest, daß der Sinus nur vom Winkel 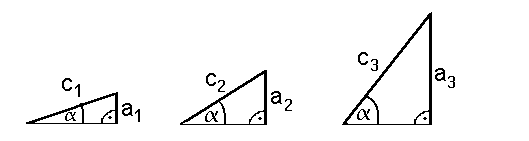a-g-alpa.pcx (200 Byte) abhängig ist:.
      tr1s0p2.pcx (3922 Byte)
a-absatz.pcx (280 Byte)Der Cosinus
      Das nächste Seitenverhältnis, daß wir kennenlernen wollen, ist
      das Verhältnis von Ankathete zur Hypothenuse (im Bild b/c):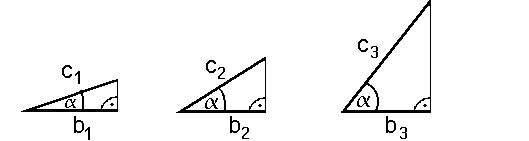
      tr2s0p3.pcx (3244 Byte)
       Dieses Seitenverhältnis nennt man den Cosinus. Der Cosinus ist
       (nur) vom Winkel a-g-alpa.pcx (200 Byte) abhängig ist, was man im Bild sehr schön sieht.

a-absatz.pcx (280 Byte)Die Cosinustabelle
      Im Kapitel Trigonometrie I haben wir eine Sinustabelle erstellt. Das
      gleiche kann man auch für den Cosinus machen. Die Cosinustabelle:
       a-g-alpa.pcx (200 Byte) 0° 10° 20° 30° 40° 50° 60° 70° 80° 90°
   Ankathete 
Hypothenuse		 1 0,98 0,94 0,87 0,77 0,64 0,5 0,34 0,17 0

     Exemplarisch zeigen wir, wie der Cosinus von 20° ermittelt wird:

           1. Man zeichnet ein rechwinkliges Dreieck, mit einem 20° Winkel:
           tr1s9p1.pcx (2250 Byte)
           2. Nun mißt man die Ankathete von a-g-alpa.pcx (200 Byte) und die Hypothenuse:
               b= 52mm             c=55mm

           3. Nun teilt man die Ankathete von a-g-alpa.pcx (200 Byte) durch die Hypothenuse,
               und erhält den Cosinus von 20°:
             tr1s9p2.pcx (2610 Byte)