Trigonometrie II                                             ZURÜCK
Der Tangens
a-absatz.pcx (280 Byte) Der Tangens
  Das vorletzte Seitenverhältnis, das wir kennenlernen wollen,
ist das Verhältnis von Gegenkathete zur Ankathete (im Bild a/b):
tr2s0p3.pcx (3244 Byte)
Dieses Seitenverhältnis nennt man den Tangens. Der Tangens ist
(nur) vom Winkel a-g-alpa.pcx (200 Byte) abhängig ist, was man im Bild sehr schön sieht.
   
a-absatz.pcx (280 Byte) Die Tangenstabelle
  Nachdem wir bereits eine Sinus- und der Cosinustabelle erstellt haben,
wollen wir nun eine Tabelle des Tangens erstellen:
          a-g-alpa.pcx (200 Byte) 0° 10° 20° 30° 40° 50° 60° 70° 80° 90°
Gegenkathete
  Ankathete		 0 0,18 0,36 0,58 0,84 1,19 1,73 2,74 5,67 ---

Exemplarisch zeigen wir, wie der Tangens von 20° ermittelt wird:

1. Man zeichnet ein rechwinkliges Dreieck, mit einem 20° Winkel:
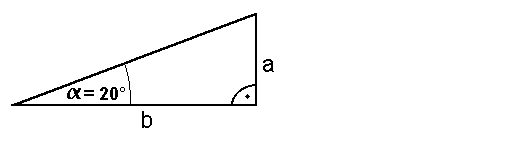
       tr1s9p1.pcx (2250 Byte)
2. Nun mißt man die Gegenkathete von a-g-alpa.pcx (200 Byte), und die Ankathete von a-g-alpa.pcx (200 Byte):

          a= 19mm             b=52mm

3. Nun teilt man die Gegenkathete vona-g-alpa.pcx (200 Byte) durch die Ankathete
    von a-g-alpa.pcx (200 Byte), und erhält den Tangens von 20°:
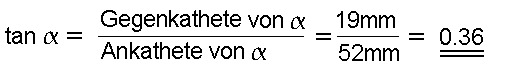
               tr1s9p2.pcx (2610 Byte)
 
a-absatz.pcx (280 Byte) Anwendungen der Tangenstabelle
  Anwendungen der Sinus-, Cosinus und Tangenstabelle folgen am Ende
des Kapitel (unter Übungen).