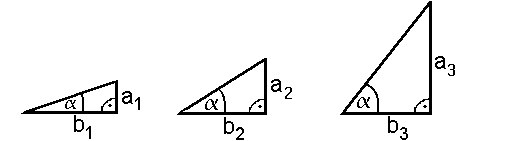| Der Cotangens |
 Der Cotangens (manchmal "Kotangens"
geschrieben)
Das letzte
Seitenverhältnis, daß wir kennenlernen wollen, ist
das Verhältnis von Ankathete zur Gegenkathete (im
Bild b/a):
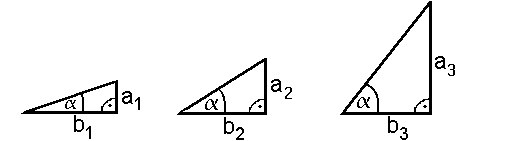
Dieses
Seitenverhältnis nennt man Cotangens. Der Cotangens ist
(nur) vom Winkel  abhängig ist, was man im Bild sehr schön
sieht.
|
|
Die Cotangenstabelle |
| |
Nach der Sinus-, der Cosinus und der
Tangenstabelle, wollen wir
nun eine Tabelle des Cotangens erstellen:
|
|
0° |
10° |
20° |
30° |
40° |
50° |
60° |
70° |
80° |
90° |
Ankathete
Gegenkathete |
--- |
5,67 |
2,74 |
1,73 |
1,19 |
0,84 |
0,58 |
0,36 |
0,18 |
0 |
Exemplarisch
zeigen wir, wie der Cotangens von 20° ermittelt wird:
1. Man zeichnet ein
rechwinkliges Dreieck, mit einem 20° Winkel:
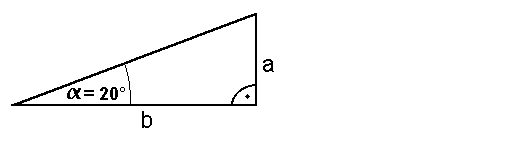
2. Nun mißt man die
Gegenkathete und die Ankathete von :
a= 19mm
b=52mm
3. Nun teilt man die
Ankathete von
durch die Gegenkathete
von , und erhält den
Cotangens von 20°:
|
Tangens und
Cotangens
Während der
Tangens das Verhältnis "Gegenkathete zur Ankathete"
ist, ist der Cotangens das Verhältnis "Ankathete zur
Gegenkathete".
Der Cotangens ist also einfach nur der Kehrwert des
Tangens,
d.h. es gelten folgende zwei Gleichungen:
|