Version: Test
©Raddy '99

Inhalt zu: Trigonometrie III         ZURÜCK
Info-Seite Vorkenntnisse: ...      Themen:   ...     Infos: www.mathematik.net
Einheitskreis Ein Kreis mit dem Radius 1, nennt man einen Einheitskreis
Sinus und Cosinus
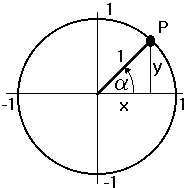am Einheitskreis		 tr3s0p1.pcx (4820 Byte)Die y-Koordinate von P nennt man Sinus a-g-alpa.pcx (200 Byte)
Die x-Koordinate von P nennt man Cosinus a-g-alpa.pcx (200 Byte)
Übungen 4 Übungsaufgaben
Lösungen Die Lösungen zu diesen Aufgaben
Negative Winkel sin (-a-g-alpa.pcx (200 Byte)) = sin (360°-a-g-alpa.pcx (200 Byte))          cos (-a-g-alpa.pcx (200 Byte)) = cos (360-a-g-alpa.pcx (200 Byte))
Winkel >360° sin (n·360°+a-g-alpa.pcx (200 Byte)) = sin a-g-alpa.pcx (200 Byte)          cos (n·360°+a-g-alpa.pcx (200 Byte)) = cos a-g-alpa.pcx (200 Byte)
Zusammenhang mit
alter Definition		 Die alte Definition (sin a-g-alpa.pcx (200 Byte) = Gegenkathete a-g-alpa.pcx (200 Byte)/Hypothenuse) aus dem
Kapitel 1 wiederspricht nicht der neuen Definition am Einheitskreis.
Gleiches gilt für die "alte" Definition des Cosinus.
Bestimmung
von a-g-alpa.pcx (200 Byte) aus sin a-g-alpa.pcx (200 Byte)		 Die Definition des "Sinus am Einheitskreis" ordnet einen
bestimmten Wert sin a-g-alpa.pcx (200 Byte)  mehrere Winkel zu.
Bestimmung
von a-g-alpa.pcx (200 Byte) aus cos a-g-alpa.pcx (200 Byte)		 Die Definition des "Cosinus am Einheitskreis" ordnet einen
bestimmten Wert cos a-g-alpa.pcx (200 Byte) mehrere Winkel zu.
Sinusfunktion Durch die Definition "Sinus am Einheitskreis" entsteht eine Funktion.
Graph der
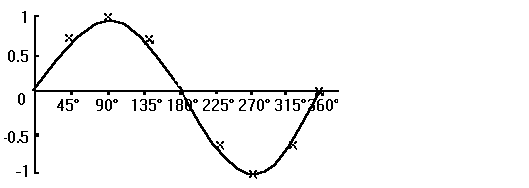Sinusfunktion		   tr3s0p1.pcx (4820 Byte)
Eigenschaften Die Sinusfunktion ist eine ungerade Funktion mit einer Periode von 360°.
Cosinusfunktion Durch die Definition "Cosinus am Einheitskreis" entsteht eine Funktion.
Graph der Cosinusfunktion 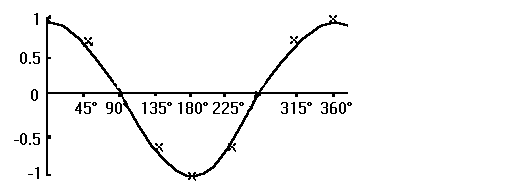tr3s0p3.pcx (3948 Byte)
Eigenschaften Die Cosinusfunktion ist eine gerade Funktion mit einer Periode von 360°.