Rückblick
Zuerst wollen wir wiederholen, was wir in diesem Kapitel
bis jetzt gelernt haben. Wir befaßten uns mit zwei Dingen:
Durch die Definition des Sinus am Einheitskreis kann man
jedem Winkel eindeutig einen Wert (Sinus genannt) zuordnen.
Eine eindeutige Zuordnung hatten wir Funktion genannt.
Umgekehrt kann man jedem Sinuswert (z.B. sin=0.9) einen
Winkel zuordnen. Wie wir auf der vorigen Seite sahen, ist
diese Zuordnung aber nicht eindeutig, also nur eine Relation.
Die Sinusfunktion
Wir wollen nun Punkt näher betrachten. Wie gesagt haben wir
durch die Definition "Sinus am Einheitskreis" jedem Winkel
eindeutig einen (Sinus genannten) Wert zuordnet. Da diese
Zuordnung eindeutig ist, ist sie eine Funktion. Wir nennen sie
Sinusfunktion. Wir fassen zusammen:
Durch die am Anfang des Kapitels
gemachte Definition
des "Sinus am Einheitskreis" wird eine Funktion definiert,
die man Sinusfunktion nennt.
Der Graph der Sinusfunktion
Der Graph der Sinusfunktion hat folgendes Bild:
Wie man den Graphen erstellt, zeigen wir auf der nächsten Seite.
Rückblick
Zuerst wollen wir wiederholen, was wir in diesem Kapitel
bis jetzt gelernt haben. Wir befaßten uns mit zwei Dingen:
Durch die Definition des Sinus am Einheitskreis kann man
jedem Winkel 
eindeutig einen Wert (Sinus genannt) zuordnen.
Eine eindeutige Zuordnung hatten wir Funktion genannt.
Umgekehrt kann man jedem Sinuswert (z.B. sin=0.9) einen
Winkel 
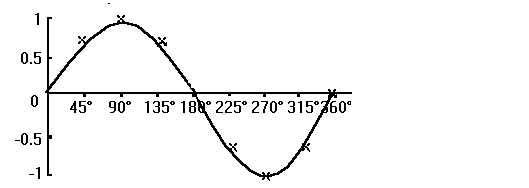Wie man den Graphen erstellt, zeigen wir auf der nächsten Seite.