Zusammenhang
mit alter
Definition |
 Die Problemstellung
Im Kapitel I definierten wir den Begriff "Sinus" am recht-
winkligen Dreieck (sin  = Gegenkathete von : Hypothenuse).
In diesem Kapitel definierten wir den Begriff des Sinus
nochmals, nämlich am Einheitskreis (sin = y-Koordinate).
Wir zeigen nun, daß die neue Definition des Sinus
(Definition am Einheitskreis) eine Erweiterung der alten
Definition (Definition am rechtwinkligen Dreieck) ist:
Der Zusammenhang
Im folgenden Bild ist ein rechtwinkliges Dreieck in den
Einheitskreis eingezeichnet, wobei 0°<<90° sein soll:
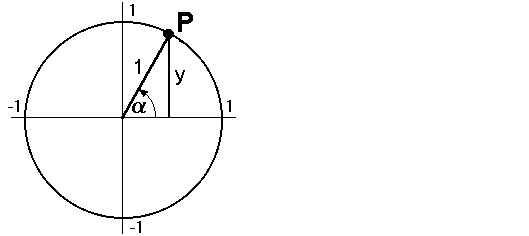Laut alter Definition aus Kapitel I gilt in diesem Dreieck:
sin = Gegenkathete von / Hypothenuse
Die Hypothenuse hat den Wert 1, also gilt:
sin = Gegenkathete von
Die Gegenkathete ist aber, wie man den Bild entnehmen kann,
gleich dem y-Koordinate des Punktes P:
sin = y-Koordinate des Punktes P
Dies ist aber auch die neue Definition des Sinus (Definition am
Einheitskreis) womit die Gleichheit der beiden Definitionen für
0°<<90° bewiesen ist.
Die neue Definition (am Einheitskreis) ordnet aber auch Winkeln
über 90° einen Sinuswert zu, während bei der alten Definition
(am rechtwinkligen Dreieck) keine Winkel über 90° vorkommen
(weil im rechtwinkligen Dreieck kein Winkel größer 90° ist).
Die neue Definition ist also eine Erweiterung der alten Definition.
|