| Der Sinussatz |
 Vorbemerkung
Bis jetzt haben wir nur rechtwinklige Dreiecke berechnet.
In diesem Kapitel wollen wir nun beliebige Dreieck berechnen.
Um beliebige Dreiecke zu berechnen braucht man den Sinus- und
den Cosinussatz. Welchen der beiden Sätze man jeweils benutzen
muß hängt davon ab, welche Seiten und Winkel gegeben sind.
Manchmal muß man sogar beide Sätze benutzen. Vorbemerkung
Bis jetzt haben wir nur rechtwinklige Dreiecke berechnet.
In diesem Kapitel wollen wir nun beliebige Dreieck berechnen.
Um beliebige Dreiecke zu berechnen braucht man den Sinus- und
den Cosinussatz. Welchen der beiden Sätze man jeweils benutzen
muß hängt davon ab, welche Seiten und Winkel gegeben sind.
Manchmal muß man sogar beide Sätze benutzen.
 Der Sinussatz Der Sinussatz
 Bild zum Sinussatz
Die obige Formel gilt natürlich nur, wenn man die Seiten
und Winkel so bezeichnet, wie es in der Geometrie üblich ist:
Der Seite a liegt der Winkel Bild zum Sinussatz
Die obige Formel gilt natürlich nur, wenn man die Seiten
und Winkel so bezeichnet, wie es in der Geometrie üblich ist:
Der Seite a liegt der Winkel  gegenüber, der Seite b liegt
der Winkel gegenüber, der Seite b liegt
der Winkel 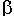 gegenüber, und der Seite c liegt gegenüber, und der Seite c liegt  gegenüber: gegenüber:

 Alternative Schreibweise des Satzes
Stellt man die Formel des Sinussatz um, so erhält man: Alternative Schreibweise des Satzes
Stellt man die Formel des Sinussatz um, so erhält man:
 Da nun die Seiten und die Sinus der Winkel ins Verhältnis gesetzt
sind, kann man den Sinussatz nun "sprachlich elegant" formulieren:
Die Seiten verhalten sich zueinander wie die Sinus
der gegenüber liegenden Winkel.
Da nun die Seiten und die Sinus der Winkel ins Verhältnis gesetzt
sind, kann man den Sinussatz nun "sprachlich elegant" formulieren:
Die Seiten verhalten sich zueinander wie die Sinus
der gegenüber liegenden Winkel.
|