Ungleichungen mit
zwei Variablen |
 |
Vorwort |
|
Bevor wir Ungleichungssysteme mit zwei Variablen behandeln,
müssen wir
erklären, was eine Ungleichung mit zwei Variablen ist, und wie
ihre
Lösungsmenge aussieht. Dazu dient diese Seite.
|
 |
Die Art der Lösungsmenge |
|
In den vorigen Kursen haben wir nur
Ungleichungen mit einer Variablen
(meist x genannt) kennengelernt. Beispiel:
x +2 < 3
(I)
Die Lösungsmenge war ein Intervall auf dem Zahlenstrahl, im Beispiel
L={x|x<1}.
Alle Zahlen in diesem
Intervall erfüllen die Lösung.
Bei einer Ungleichung mit zwei Variablen
treten zwei Variablen auf,
die meist mit x und y bezeichnet werden:
2y +6 < 2x (II)
Bevor wir die Lösungsmenge ermitteln, wollen wir zunächst über die Art
der Lösungsmenge besprechen. Die Lösungsmenge besteht nicht mehr aus
Zahlen,
sondern aus Zahlenpaaren.
Setzen wir z.B. x=10 und y=1 in die Ungleichung II ein,
so erhalten wir eine wahre Aussage, und daher ist das Zahlenpaar (10 /1)
eine Lösung
der Ungleichung:
2·1 +6 < 2·10
8 < 20
Die Lösungsmenge einer Ungleichung besteht also aus Zahlenpaare.
Zahlenpaare
kann man aber nicht mehr auf der Zahlengeraden darstellen, sondern durch
Punkte in der Ebene (im rechtwinkligen Koordinantensystem).
|
 |
Ermitteln der Lösung |
|
Zur Erinnerung: Gegeben war eine Ungleichung mit zwei Variablen:
2y +6 < 2x
Um nun die Lösungsmenge einer Ungleichung mit zwei Variablen zu
ermitteln, stellt
man die Ungleichung zunächst nach y um. Im Beispiel müssen wir zu diesem
Zweck
die Ungleichung durch 2 teilen:
y +3 < x
und dann 3 subtrahieren:
y < x–3
Wir interpretieren jetzt die rechte Seite der Ungleichung als Funktion
f(x)=x–3,
und zeichnen die Funktion in ein Koordinantensystem mit den Achsen x
und y:
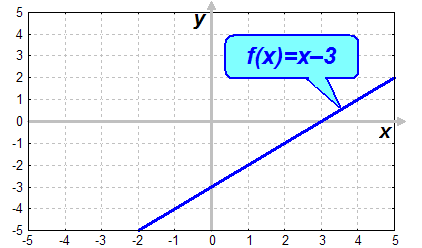
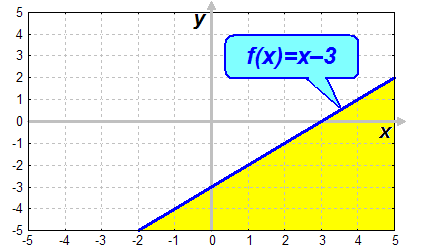
Die Ungleichung y < x–3 bedeutet nun: Wann ist y kleiner als
der Funktionswert
der Funktion f(x) = x–3, d.h. welche Punkte liegen unterhalb des Graphen
der
Funktion f(x)=x–3. Es sind alle Punkte in der gelb eingezeichneten
Fläche:
 |
| |
|