Ungleichungssysteme
mit
zwei Variablen |
 |
Definition |
|
Wir wissen bereits aus Kapitel 1, dass die Lösungen eines Ungleichungssystem
alle Ungleichungen des Systems erfüllen müssen.
Das Besondere an einem Ungleichungssystem mit zwei Variablen
ist eben nur,
dass die Ungleichungen des Systems Ungleichungen mit zwei Variablen
sind,
also Ungleichungen,
die wir auf den vorigen Seiten kennengelernt haben:
Ein Ungleichungssystem mit zwei Variablen besteht aus
mindestens zwei Ungleichungen,
wobei in den Ungleichungen insgesamt 2 Variablen (meist x und y
genannt) vorkommen.
Die Lösungsmenge besteht aus den Zahlenpaaren, die alle
Ungleichungen erfüllen. |
Anmerkung 1: Nicht in allen Ungleichungen müssen beide
Variablen vorkommen.
Anmerkung 2: Man macht unterhalb und rechts der
Ungleichungen einen Rahmen,
um anzudeuten, dass es sich um ein System von Ungleichungen
handelt,
und nicht um einzelne Ungleichungen.
Anmerkung 3: Da Ungleichungen mit zwei Variablen Zahlenpaare
als Lösung haben,
besteht die Lösung eines Ungleichungssystems mit zwei
Variablen
natürlich ebenfalls aus Zahlenpaaren.
|
|
 |
Beispiele |
|
Das folgende System ist ein Ungleichungssystem mit zwei Variablen:
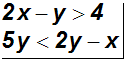
Wie gesagt brauchen nicht beide Variablen in allen Ungleichungen
vorkommen, und
daher ist auch das folgende System ein Ungleichungssystem mit zwei
Variablen:
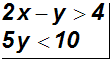
Wie gesagt besteht die Lösung aus allen Zahlenpaaren, die beide
Ungleichungen erfüllen.
|
| |
|