Version: Test
©Raddy 2000

Vektorräume I                                             ZURÜCK
Ein Beispiel:
Der Vektorraum
der 2x2Matrizen		 a-absatz.pcx (280 Byte)Beispiel: 2x2 Matrizen
       Auf der vorigen Seite haben wir gelernt, daß ein Vektorraum
       aus drei Dingen besteht:

           a-1.pcx (190 Byte) Kommutative Gruppe G
           a-2.pcx (192 Byte) Körper K
           a-3.pcx (194 Byte) Verknüpfung S zwischen Gruppen- und Körperelementen,
               die die Axiome S1-S5 erfüllen muß

       In diesem Kapitel wollen wir nur einen einzigen Vektorraum
       kennenlernen, diesen aber gründlich erforschen. Es ist der
       Vektorraum der 2x2 Matrizen. Auch in diesem Vektorraum
       muß es natürlich die oben genannten "drei Dinge" geben.
       Wir wählen also eine Gruppe G, einen Körper K und eine
       Verknüpfung:
        
           zu a-1.pcx (190 Byte) Die Gruppe der 2x2 Matrizen (s.Kapitel Gruppen I)
           zu a-2.pcx (192 Byte) Den Körper der reellen Zahlen (s.Kapitel Körper I)
           zu a-3.pcx (194 Byte) Die Verknüpfung S müssen wir noch definieren:

a-absatz.pcx (280 Byte)Die Verknüpfung S
       Nun müssen wir nur noch eine Verknüpfung S finden, welche
       die Gruppen- und Körperelemente miteinander verknüpft.
       Wir brauchen jedoch nicht lange suchen, denn eine solche
       Verknüpfung haben wir schon im Kapitel Matrizen II definiert, 
       und sie damals Skalar-Matrix-Multiplikation genannt.
       Die Verknüpfung lautete:

            Eine Skalar a-g-alpa.pcx (200 Byte) (Skalar=Körperelement) wird mit einer Matrix
            multipliziert, indem jedes Element der Matrix mit dem Skalar
            (reelle Zahl) multipliziert wird: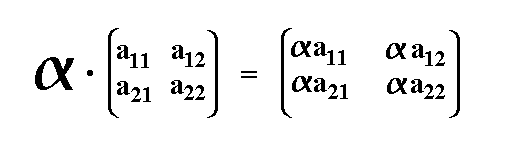
      vr1s4p1.pcx (4911 Byte)
       Nun haben wir schon fast einen Vektorraum konstruiert.
       Wir müssen aber noch überprüfen, ob die Verknüpfung S
       die Axiome (S1-S5) erfüllt. Davon handeln die nächsten
       Seiten dieses Kapitels.