Gegeben sei ein Vektorraum V und eine Basis  B= {v₁ ... v_n}
       dieses Vektorraumes. Nun möchten wir aber, daß ein beliebiger
       Vektor w auch zu Basis gehört, d.h. wir möchten einen der
       Vektoren v durch den Vektor w austauschen, sodaß eine neue
       Basis entsteht, in der auch w enthalten ist.

       Es entsteht die Frage: Findet man immer einen Vektor v aus B,
       den man durch w ersetzen kann, und wenn ja, welcher ist es?
       Die Antwort gibt diese und die nächste Seite:

Gegeben sei ein Vektorraum V, eine Basis B= {v1 ... vn} von V und ein beliebiger Vektor w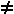0 des Vektorraumes V. Dann gilt:    Fügt man den Vektor w zur Basis B hinzu, und entfernt man    im Gegenzug einen geeigneten* Vektor aus der Basis B,    so erhält man eine neue Basis des Vektorraumes V.    Dabei gilt: Es gibt immer mindestens einen  Vektor v aus B    der geeignet ist, um gegen w ausgetauscht zu werden.

      *Welcher Vektor geeignet ist, zeigt die nächste Seite

Beispiel
 

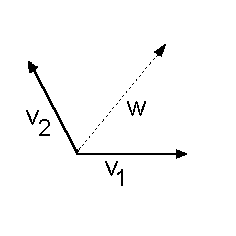	Gegeben sei der geometrische Vektorraum der Ebene und eine Basis B1 = {v1, v2} desselben Vektorraumes. Außerdem sei noch ein beliebiger Vektor w des Vektorraumes V gegeben, der nicht zur Basis gehört
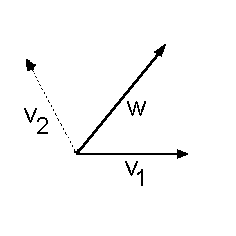	Nun entfernen wir v2 aus der Basis und fügen w zur Basis dazu. Es entsteht die neue Basis B2 = {v1, w} v2 ist also geeignet, um gegen w ausgetauscht zu werden.