Wahl des Austauschvektor
|
 Einführung in die Fragestellung Einführung in die Fragestellung
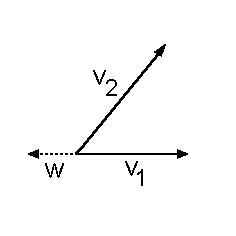 Gegeben sei der
geometrische Gegeben sei der
geometrische
Vektorraum der Ebene und eine
Basis B1 = {v1, v2} desselben
Vektorraumes.
Außerdem sei noch ein Vektor w des Vektorraumes
V gegeben,
der nicht zur Basis gehört
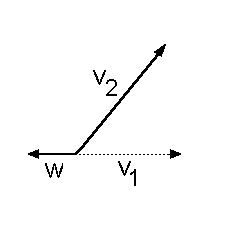 Nun entfernen wir v1 aus der Nun entfernen wir v1 aus der
Basis und fügen w zur Basis
dazu. Es entsteht die neue
Basis B2 = {v2, w} der
Ebene.
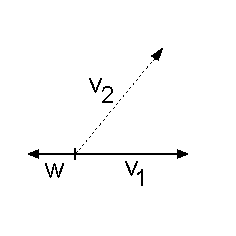 Nun zum Gegenbeispiel: Nun zum Gegenbeispiel:
Entfernen wir v2 aus der Basis
und fügen w hinzu, so erhalten
wir die Menge {v1, w}.
Dies ist nun aber keine (!)
Basis der Ebene mehr, denn
die beiden Vektoren sind
kollinear.
 Formel Formel
Aufgrund
dieses Beispiels stellt sich die Frage, welche Vektoren
einer Basis geeignet sind, um gegen einen beliebigen
Vektor w
ausgetauscht zu werden. Es sind dies die Vektoren,
die in der
Linearkombination:
w = k1·v1
+ k2·v2 + ... + kn·vn
einen Koeffizienten ki haben, der von Null
verschieden ist.
Überprüfen wir dies an unserem Beispiel: w = 0.25·v1
+ 0·v2
Also dürfen wir v1 durch w ersetzen, aber nicht v2
.
|
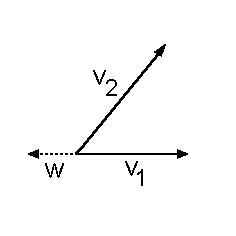
 Nun entfernen wir v
Nun entfernen wir v Nun zum Gegenbeispiel:
Nun zum Gegenbeispiel: