Steinitz'scher
Austauschsatz |
 Steinitz'scher Austauschsatz Steinitz'scher Austauschsatz
Gegeben
seien:
1. Ein Vektorraum V
2. Eine Basis B dieses Vektorraumes: B = {b1 ... bn}
3. Eine linear unabhängige Menge A aus Vektoren
dieses Vektorraumes: A = {a1 ... am}
Daraus folgt:
1. n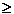 m m
2. Fügt man zur Basis B = {b1 ... bn} die linear
unabhängige
Menge A = {a1 ... am} hinzu,
und entfernt im Gegenzug
m Vektoren aus der Basis b, so erhält man eine
neue Basis B':
B' = {b1
... bn} 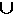 {a1 ... am} - {m Vektoren aus B} {a1 ... am} - {m Vektoren aus B}
oder
B' = {n-m
Vektoren aus B} 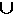 {a1 ... am} {a1 ... am}
|
 Anmerkungen zum
Satz Anmerkungen zum
Satz
 Der Steinitz'sche
Austauschsatz sagt nur, daß es Der Steinitz'sche
Austauschsatz sagt nur, daß es
m geeignete Vektoren in B
gibt, die man gegen {a1 ... am}
austauschen kann. Der
Steinitz'sche Austauschsatz
sagt aber nicht, welche
Vektoren geeignet sind.
 Der Ausdruck B'
= {n-m Vektoren aus B} Der Ausdruck B'
= {n-m Vektoren aus B} 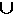 {a1 ... am} {a1 ... am}
wird in der Regel einfacher
geschrieben. Dazu nummeriert
man die übriggebliebenen n-m
Vektoren der Basis B um,
und gibt
ihnen die Indizes bm+1 ... bn :
B' = {a1 ... am, bm+1 ... bn}
|