Version: Test |
Vektorräume V ZURÜCK |
| Beispiel zum Steinitz'schen Austauschsatz: |
Gegeben sei der dreidimensionale Raum und eine Basis B = {b1,b2,b3} dieses Raumes: 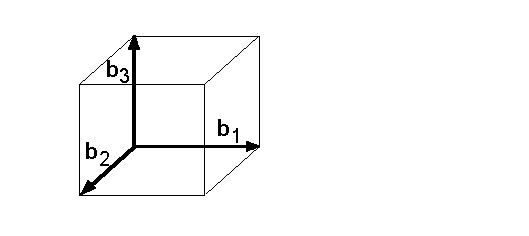 Außerdem sei die linear unabhängige Menge {c1,c2} gegeben: 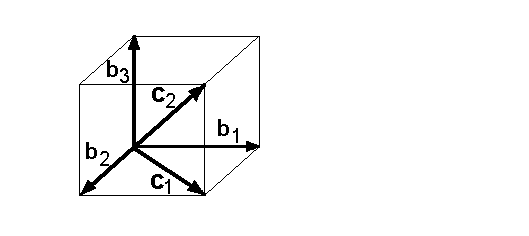 Laut Teil 1 des Steinitz'schen Austauschsatzes hat die linear unabhängige Menge {c1,c2} weniger (oder gleich viel) Vektoren wie die Basis B hat: Laut Teil 2 des Satzes erhält man eine weitere Basis B', indem man die Vektoren {c1,c2} zur Basis B hinzufügt, und im Gegenzug zwei geeignete Vektoren aus der Basis entfernt werden. Geeignet sind z.B. die Vektoren {b2,b3}. Die neue Basis B' lautet dann B'={b1, c1,c2}: 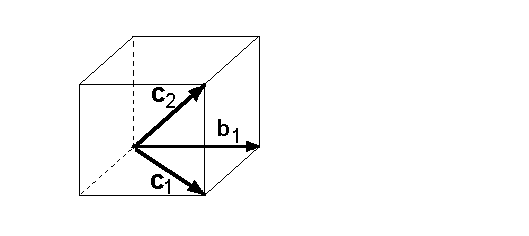 |