Version: Test |
Vektorräume V ZURÜCK |
| Gegenbeispiel zum Steinitz'schen Austauschsatz: |
 Die ProblemstellungBis jetzt haben wir den Steinitz'schen Austauschsatz kennengelernt. Er lautete: Sind eine Basis B aus n Vektoren und eine linear unabhängige Menge aus m Vektoren gegeben, so erhält man eine weitere Basis B' dieses Vektorraumes, indem man: 1. Die m Elemente der Menge C zur Basis B hinzufügt. 2. m geeignete Vektoren aus B entfernt Nun zu Schritt 2: Enfernt man stattdessen nicht geeignete Vektoren, so erhält man keine neue Basis. Dazu ein Beispiel: BeispielGegeben seien die gleichen Vektoren wie auf der vorigen Seite also die gleiche Basis B = {b1,b2,b3} und die gleiche linear unabhängige Menge {c1,c2}: 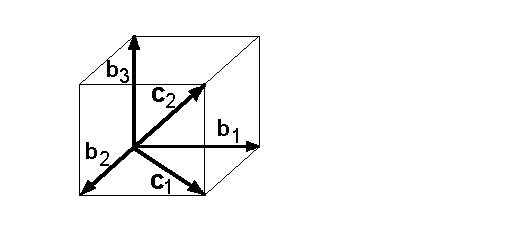 Auf der vorigen Seite haben wir die Vektoren {b2,b3} entfernt und die Vektoren {c1,c2} hinzugefügt. Als Folge erhielten wir eine weitere Basis B' des Vektorraumes Nun wollen wir stattdessen die Vektoren {b1,b2} entfernen und die Vektoren {c1,c2} hinzufügen. Als Folge erhalten wir keine Basis, denn die drei Vektoren sind komplanar: 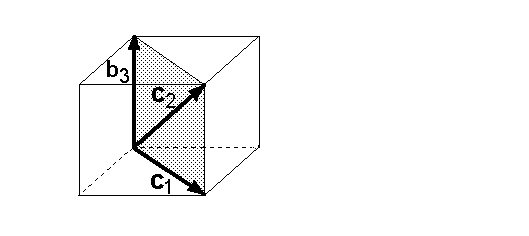 |