Version: Test
©Raddy 2000

Vektorräume V                                             ZURÜCK
Alternative
Formulierung des
Steinitz'schen
Austauschsatzes		 a-absatz.pcx (280 Byte)Alternative Formulierung des
    Steinitz'schen Austauschsatzes
       Man kann den Steinit'schen Austauschsatz auch etwas
       anders formulieren. Man beachte das beiden Formulierungen
       den gleichen Satz wiederspiegeln:
Gegeben seien:

   1. Ein Vektorraum V
   2. Eine Basis B dieses Vektorraumes: B = {b1 ... bn}
   3. Eine linear unabhängige Menge A aus Vektoren
       dieses Vektorraumes: A = {a1 ... am}

Daraus folgt:

   1. n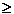a-gr-gl.pcx (207 Byte)m

  2.  Jede linear unabhängige Menge A = {a1 ... am} kann
       durch Hinzunahme geeigneter Vektoren aus einer
       Basis  B = {b1 ... bn} zu einer Basis B' ergänzt
       werden:  B' = {a1 ... am , bm+1 ... bn}