| Dimension |
 Satz Satz
Alle Basen
eines bestimmten Vektorraumes
haben gleich viele Elemente |
 Beweis Beweis
Der
Beweis erfolgt mit Hilfe des Steinitz'schen Austauschsatzes.
Die Basen B und C seien Basen desselben Vektorraumes.
Weil jede Basis auch laut ihrer Definition eine
linear unabhängige
Menge ist, kann z.B. die Basis B die Rolle der linear
unabhängigen
Menge im Steinitz'schen Austauschsatz übernehmen:
|B|
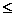 |C| |C|
Andererseits
kann man die Basis C die Rolle der linear
unabhängigen Menge im Steinitz'schen Austauschsatz
übernehmen lassen:
|C|
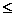 |B| |B|
Faßt man
beiden Aussagen zusammen, so bedeutet dies:
|B|
= |C|
was zu beweisen
war.
 Dimension Dimension
Im Satz oben
haben wir gesagt, daß alle Basen eines
bestimmten Vektorraumes gleich viele Vektoren haben.
Man nennt diese Anzahl der Basisvektoren die
Dimension dieses Vektorraumes. Die Dimension
eines Vektorraumes ist seine wichtigste Kenngröße.
|