Version: Test
©Raddy 2000

Vektorräume VI                                         ZURÜCK

Gegeben sei ein Vektorraum V
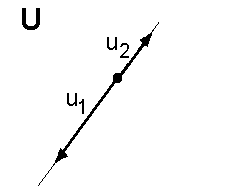und ein Unterraum U. Im Beispiel
sei  der geometrische Vektorraum
der Ebene gegeben und der ein-
gezeichnete Unterraum, den wir
aus dem vorigen Kapitel kennen.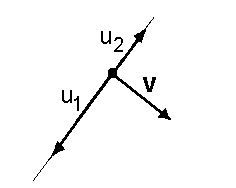



Außerdem sei ein beliebiger
Vektor v des Vektorraumes V
gegeben.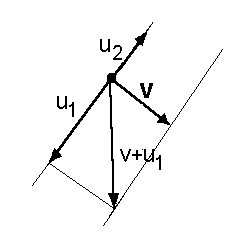






Nun wählen wir einen beliebigen
Vektor uU, im Bild wählen wir  u₁.
Zu diesem Vektor addieren wir den
Vektor v hinzu. Wir erhalten den
Vektor v+u₁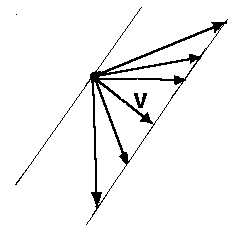






Das gleiche machen wir mit allen
anderen Vektoren aus U. Zu jedem  
Vektor u aus U addieren wir v hinzu.

Es ensteht die Nebenklasse v+U.
Der Vektor v nennt sich Repräsentant
der Nebenklasse v+U. Die Elemente
der Nebenklasse v+U sind die Vektoren
v+u₁ , v+u₂ , v+u₃ ,  ....

Definition der Nebenklasse
       Sei U ein Unterraum von V. Addiert man einen Vektor vV
       zu jedem Element uU hinzu, so entsteht die Nebenklasse v+U,
       die aus den Elementen v+u₁ , v+u₂ , v+u₃ ,  .... besteht.