2.Teil Beweis:
Gleichheit von
Nebenklassen |
 2.Teil des Beweis 2.Teil des Beweis
Nun müssen wir noch "in die andere Richtung" beweisen, d.h. wir
wollen beweisen: Wenn v-w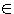 U, dann gilt: v+U = w+U U, dann gilt: v+U = w+U
 Laut Voraussetzung ist v-w Laut Voraussetzung ist v-w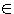 U, d.h. es gibt ein u0
mit v-w=u0 U, d.h. es gibt ein u0
mit v-w=u0
Indem wir die diese Formel
umstellen, können wir die
Voraussetzung auch anders
schreiben: v = u0+w
 Nun zum Beweis: Die Nebenklasse v+U
kann man Nun zum Beweis: Die Nebenklasse v+U
kann man
auch folgendermaßen
schreiben:
|
|
|
v+u |
mit: u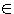 U U |
|
|
Den Vektor v dürfen wir nach Voraussetzung
durch u0+w ersetzen: |
|
|
|
u0+w+u |
mit: u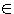 U U |
|
|
Die Menge u0+w+u mit: u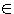 U ist Teilmenge von w+U, U ist Teilmenge von w+U,
denn jeder Vektor u0+u ist wegen der "Abgeschlossenheit"
des Unteraumes U ein Vektor aus U: |
|
|
|
w+u0+u |
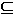 w+U w+U |
mit: u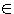 U U |
|
Den Vektor w+u0 dürfen wir nach Voraussetzung
wieder durch v ersetzen: |
|
|
|
v+u |
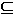 w+U w+U |
mit: u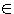 U U |
|
Das kann man nun wiederum so schreiben: |
|
|
|
v+U |
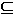 w+U w+U |
|
 Wir haben soeben bewiesen: Aus v-w Wir haben soeben bewiesen: Aus v-w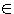 U folgt
v+U U folgt
v+U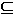 w+U . w+U .
Genauso könnte man
beweisen: Aus w-v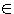 U folgt w+U U folgt w+U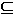 v+U v+U
Wenn aber
gilt v+U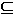 w+U und w+U w+U und w+U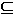 v+U , dann gilt v+U , dann gilt
v+U=w+U, was wir auf
dieser Seite beweisen wollten.
|