Wie wird aus
einer Menge ein
Vektorraum? |
 Die Problemstellung
Auf der nächsten Seite wollen wir aus einer Faktormenge
einen Vektorraum konstruieren, den sogenannten
Faktorraum.
Zur Einführung in das Thema, werden wir auf dieser
Seite
erstmal zeigen, wie man aus einer beliebigen
Menge einen
Vektorraum konstruiert:
Die
Vorgehensweise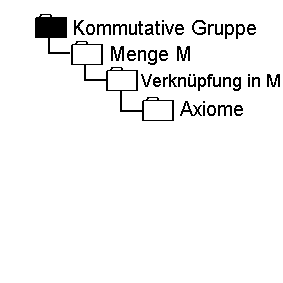
Gegeben sei eine Menge M.
Auf dieser Menge definieren wir
eine in der Menge M abgeschlossene
Verknüpfung (oft Addition genannt).
Wenn die Verknüpfung auch noch
gewisse Axiome erfüllt (z.B. das
Kommutativgesetz), dann bilden
Menge und Verknüpfung zusammen
eine kommutative Gruppe.
Die Elemente von M werden
damit zu Gruppenelementen.
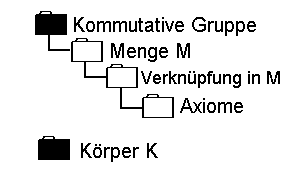 Im zweiten Schritt wählen wir
einen Körper K, z.B. den Körper
der reellen Zahlen oder der
komplexen Zahlen, oder ganz
allgemein eine nicht näher
definierten Körper K.
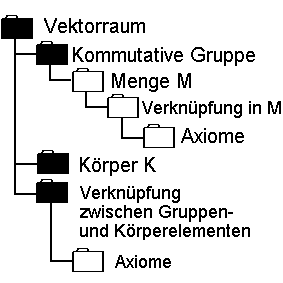 Im dritten Schritt definieren wir
eine Verknüpfung zwischen den
Elementen der Menge M und des
Körpers. Auch diese Verknüpfung
muß gewisse Axiome erfüllen.
Dadurch entsteht ein Vektorraum.
Die Elemente der Menge M nennt
man nun Vektoren.
|