| Faktorräume |
 Die Problemstellung
Auf der letzten Seite haben wir gezeigt, wie man aus einer
beliebigen Menge einen Vektorraum konstruiert.
Nun wollen wir
aus der Menge aller Nebenklassen von U (also aus V/U)
einen
Vektorraum konstruieren, den sogenannten Faktorraum:
Die
Vorgehensweise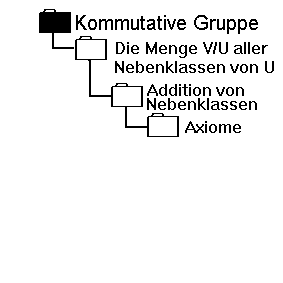
Gegeben sei die Menge V/U,
also die Menge aller Nebenklassen.
Nun müssen wir eine in der Menge
V/U abgeschlossene Verknüpfung
definieren. Wir definieren:
(v+U) + (w+U) = (v+w)+U
Die Menge V/U bildet zusammen
mit dieser Verknüpfung eine Gruppe.
Das diese Verknüpfung alle
Gruppenaxiome erfüllt, zeigen wir
auf der nachfolgenden Seite.
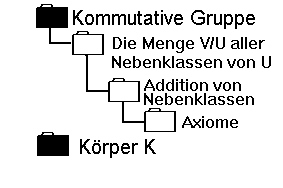 Im zweiten
Schritt wählen wir
einen Körper. Wir wählen einen
nicht näher definierten Körper K.
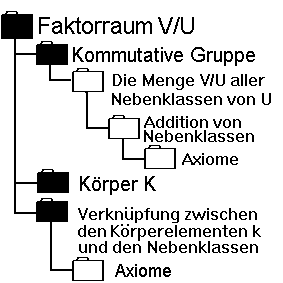 Im dritten Schritt definieren wir
eine Verknüpfung zwischen den
Elementen k des Körpers und den
Elementen der Menge V/U (also
den Nebenklassen):
k·(v+U) = (k·v)+U
Dadurch entsteht ein Vektorraum.
Die Elemente der Menge V/U, also
die Nebenklassen, nennt man nun
Vektoren.
Fazit
Durch
die Definition der "Addition von Nebenklassen" und des
"Produktes aus Skalar und Nebenklasse",
haben wir aus der
Faktormenge einen Faktorraum gemacht. |