Version: Test ©Raddy 2000	Inhalt zu: Vektoralgebra I ZURÜCK
Info-Seite	Vorkenntnisse: ... Themen: ... Infos: www.mathematik.net
Skalare und Vektoren	Ein Skalar hat einen Betrag aber keine Richtung. Beispiel: Temperatur. Ein Vektor ist eine Größe mit einem Betrag und einer Richtung. Ein Beispiel für einen Vektor ist die Windgeschwindigkeit. Vektoren werden durch Pfeile dargestellt. Das Bild links zeigt drei verschiedene Vektoren.
Genauere Definition	Unter einem Vektor versteht man die "Menge aller Pfeile" mit gleicher Richtung und gleichem Betrag.
Repräsentant des Vektors	Jeder Pfeil aus dieser Menge ist ein sogenannter Stellvertreter oder "Repräsentant des Vektors".
Schreibweisen	Ein Vektor kennzeichnet man oft durch einen Pfeil oder durch Fettdruck:
Vektoraddition	Zwei Vektoren und werden addiert, indem man zuerst den Vektor durch denjenigen seiner Repräsentanten darstellt, der am Ende von beginnt. Der Vektor + ist dann der Vektor, der am Anfang von 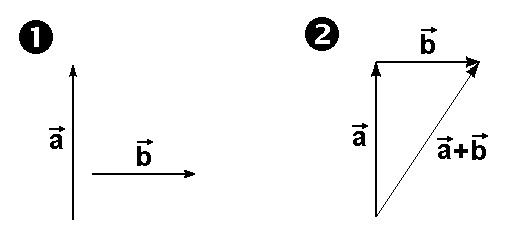beginnt und am Ende von endet:
Vektoraddition von 3 Vektoren	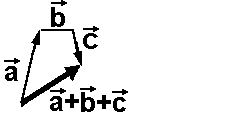Genauso wie die Addition von zwei Vektoren verläuft die Addition von drei Vektoren.
Kommutativgesetz	Die Vektoraddition ist kommutativ: + = +
Assoziativgesetz	Die Vektoraddition ist assoziativ: (+)+ = +(+)