 Kommutativgesetz
Wir haben soeben die Vektoraddition kennengelernt.
Diese Vektoradditon ist kommutativ. Das bedeutet, das
man die Reihenfolge der Summanden vertauschen darf: Kommutativgesetz
Wir haben soeben die Vektoraddition kennengelernt.
Diese Vektoradditon ist kommutativ. Das bedeutet, das
man die Reihenfolge der Summanden vertauschen darf:
 Verdeutlichung des Kommutativgesetzes Verdeutlichung des Kommutativgesetzes
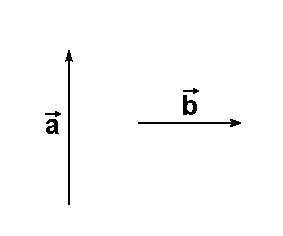 Gegeben seien wieder die beiden
Vektoren
Gegeben seien wieder die beiden
Vektoren  und und  . .
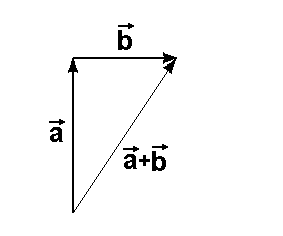 Zuerst bilden wir die Summe
Zuerst bilden wir die Summe
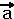 + +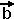 . .
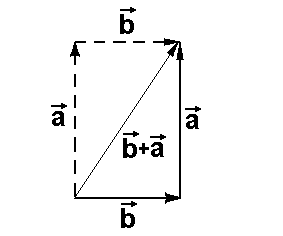 Nun bilden wir den
Vektor Nun bilden wir den
Vektor 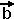 + +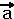 , indem wir
(wie vorgeschrieben)
an den Vektor , indem wir
(wie vorgeschrieben)
an den Vektor 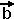 den
Vektor den
Vektor 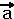 anhängen.
Am Bild sieht man dann,
daß die beiden Vektoren anhängen.
Am Bild sieht man dann,
daß die beiden Vektoren
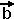 + +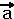 und und 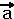 + +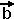 gleich sind. gleich sind.
|