Assoziativ-
gesetz der
Vektoraddition |
 Assoziativgesetz Assoziativgesetz
Wir
haben soeben gelernt, daß die Vektoraddition kommutativ
ist. Zweitens ist sie auch noch assoziativ.
Unter Assoziativität
versteht man, daß man beliebige Teilsummen zuerst
berechnen
darf, ohne das sich das Ergebnis ändert:
 Verdeutlichung
des Assoziativgesetzes Verdeutlichung
des Assoziativgesetzes
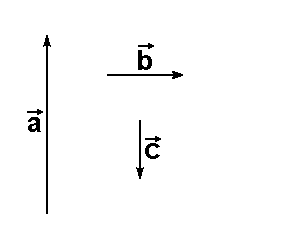
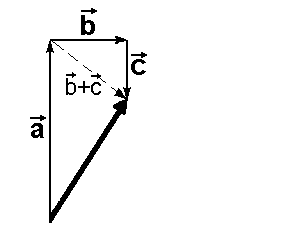
Gegeben seien die drei
Vektoren 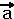 , , 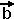 und und 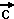 . .
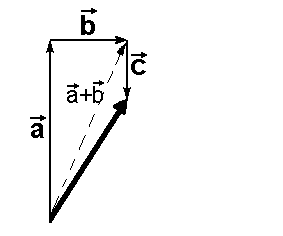
In diesem Bild bilden wir die
Summe (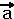 + + 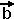 ) + ) + 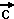 . Dazu bilden . Dazu bilden
wir zuerst (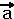 + + 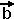 ), was durch ), was durch
die gestrichelte Linie angedeutet
ist, und addieren dazu 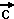 . Das . Das
Endergebnis (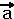 + + 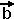 ) + ) + 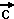 ist ist
dann der "dicke Pfeil".
 Im Gegensatz zum
vorigen Bild, Im Gegensatz zum
vorigen Bild,
wollen wir jetzt die Summe
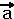 +( +(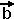 + +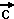 ) bilden. ) bilden.
Dazu bilden wir zuerst die Teil-
summe (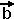 + +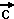 ). Das Ergebnis ist ). Das Ergebnis ist
die gestrichelte Linie. Dann führen
wir die Addition 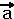 +( +(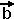 + +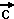 ) aus. ) aus.
Das Endergebnis ist wieder der
gleiche "dicke Pfeil" wie im
Bild zuvor.
Also haben wir gezeigt, daß man beliebige
Teilsummen zuerst
berechnen darf, d.h. wir haben gezeigt: (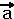 + +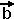 )+ )+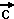 = =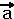 +( +(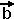 + +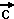 ) ) |
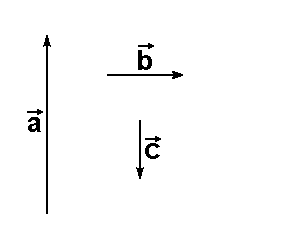

 Im Gegensatz zum
vorigen Bild,
Im Gegensatz zum
vorigen Bild,