Eigenschaft
linear
abhängiger
Vektoren |
 Satz
Der folgende Satz beschreibt eine wichtige Eigenschaft
linear abhängiger Vektoren:
Ist eine Menge {a, b, ...} linear
abhängiger Vektoren
gegeben, so kann mindestens ein Vektor als Linear-
kombination der anderen Vektoren ausgedrückt werden. |
Anmerkung
Im Satz wird gefordert, daß man mindestens einen der Vektoren
durch die anderen ausdrücken kann. Der Satz sagt jedoch nicht,
daß man jeden Vektor durch die jeweils anderen ausdrücken kann.
|
Beispiel |
| |
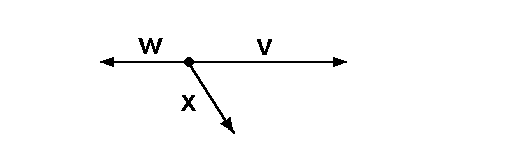
Wir wählen ein Beispiel aus der Ebene. Gegeben seien
die drei Vektoren der Ebene,
die wir v, w, x nennen: |
| |
 |
| |
1. Den Vektor v kann man durch die anderen (restlichen)
Vektoren ausdrücken: v = –2·w + 0·x
2. Auch den Vektor w kann man durch die anderen Vektoren
ausdrücken: w = –0.5·v + 0·x
3. Den Vektor x kann man nicht durch die anderen Vektoren
ausdrücken. |
|