| Nullsummen |
 Definition Definition
Eine Linearkombination 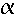 ·v + ·v + 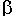 ·w + ... kann
gleich dem ·w + ... kann
gleich dem
Nullvektor sein. Die Linearkombination nennt man dann
auch eine Nullsumme. |
 Beispiel
Zuerst betrachten wir ein normale Linearkombination 1·a+2·b+1·c
Dem Ergebnisvektor geben wir den Namen x: Beispiel
Zuerst betrachten wir ein normale Linearkombination 1·a+2·b+1·c
Dem Ergebnisvektor geben wir den Namen x:
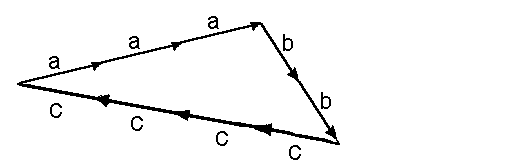
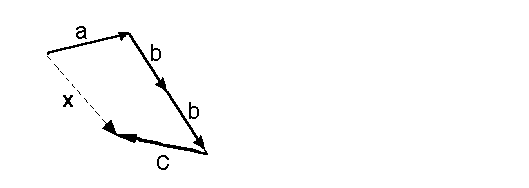 Die Linearkombination 3·a+2·b+4·c hat als Ergebnisvektor
den Nullvektor 0. Man sagt 3·a+2·b+4·c ist eine Nullsumme:
Die Linearkombination 3·a+2·b+4·c hat als Ergebnisvektor
den Nullvektor 0. Man sagt 3·a+2·b+4·c ist eine Nullsumme:
 Geschlossene Vektorketten (Streckenzüge)
Grafisch kann man eine Nullsumme daran erkennen, daß sie
eine sogenannte geschlossene Vektorkette bildet.
Man sagt statt geschlossener Vektorkette auch geschlossener
Streckenzug. Geschlossene Vektorketten (Streckenzüge)
Grafisch kann man eine Nullsumme daran erkennen, daß sie
eine sogenannte geschlossene Vektorkette bildet.
Man sagt statt geschlossener Vektorkette auch geschlossener
Streckenzug.
|