Details zu
Fall 4 |
 Fall 4
Treffen die Fälle 1 bis 3 nicht zu, so gilt für die vier
Vektoren, daß es unter ihnen drei Vektoren gibt (a,b,c),
die linear unabhängig sind, weil sie weder kollinear noch
komplanar sind, und auch der Nullvektor nicht unter ihnen zu
finden ist. Die vier Vektoren liegen dann so: Fall 4
Treffen die Fälle 1 bis 3 nicht zu, so gilt für die vier
Vektoren, daß es unter ihnen drei Vektoren gibt (a,b,c),
die linear unabhängig sind, weil sie weder kollinear noch
komplanar sind, und auch der Nullvektor nicht unter ihnen zu
finden ist. Die vier Vektoren liegen dann so:
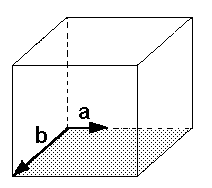 Weil a und b nicht kollinear
sind (dann läge Fall 2 vor),
spannen sie eine Ebene auf.
Diese Ebene ist gleich dem
Boden des Würfels. Weil a und b nicht kollinear
sind (dann läge Fall 2 vor),
spannen sie eine Ebene auf.
Diese Ebene ist gleich dem
Boden des Würfels.
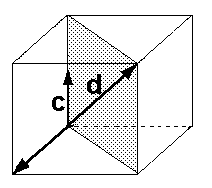 c und d liegen nicht in der von
den Vektoren a und b aufgespannten
Ebene, denn sonst hätten wir
ja Fall 3 vorliegen. Außerdem
spannen c und d eine Ebene auf,
denn sonst hätten wir Fall 2
(c und d wären kollinear). c und d liegen nicht in der von
den Vektoren a und b aufgespannten
Ebene, denn sonst hätten wir
ja Fall 3 vorliegen. Außerdem
spannen c und d eine Ebene auf,
denn sonst hätten wir Fall 2
(c und d wären kollinear).
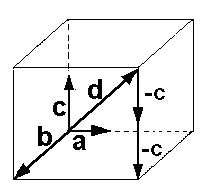 Nun versuchen wir eine nicht-
triviale Nullsumme zu bilden:
Zuerst hängen wir den Vektor c
an den Vektor d, und verlängern
den Vektor c bis er die Ebene
erreicht, die von den Vektoren
a und b aufgespannt wird. Nun versuchen wir eine nicht-
triviale Nullsumme zu bilden:
Zuerst hängen wir den Vektor c
an den Vektor d, und verlängern
den Vektor c bis er die Ebene
erreicht, die von den Vektoren
a und b aufgespannt wird.
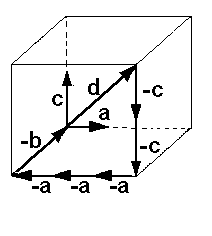 Nun hängen wir den Vektor -a
an die Vektoren -c, und verlängern -a
solange bis er die Gerade schneidet
auf der der Vektor b liegt. Achtung:
Diesen Schnittpunkt muß es geben,
denn a und b liegen ja in der gleichen
Ebene, bzw. spannen diese auf.
Nun haben wir eine nichttriviale
Nullsumme gefunden: d-2c-3a-b=0
und somit sind a,b,c,d linear abhängig. Nun hängen wir den Vektor -a
an die Vektoren -c, und verlängern -a
solange bis er die Gerade schneidet
auf der der Vektor b liegt. Achtung:
Diesen Schnittpunkt muß es geben,
denn a und b liegen ja in der gleichen
Ebene, bzw. spannen diese auf.
Nun haben wir eine nichttriviale
Nullsumme gefunden: d-2c-3a-b=0
und somit sind a,b,c,d linear abhängig.
|