Beweis
des Satz:
Betrag
eines
Vektors
der Ebene |
 Beweis
Nun wollen wir den Satz von der vorigen Seite beweisen,
mit dem man den Betrag eines Vektors der Ebene berechnen
kann. Der Satz lautete: Beweis
Nun wollen wir den Satz von der vorigen Seite beweisen,
mit dem man den Betrag eines Vektors der Ebene berechnen
kann. Der Satz lautete:
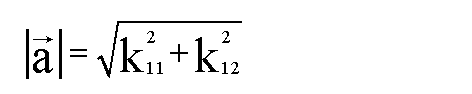 Um den Satz zu beweisen müssen wir uns ins Gedächnis rufen,
was die Koordinaten
Um den Satz zu beweisen müssen wir uns ins Gedächnis rufen,
was die Koordinaten 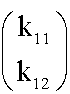 bedeuten. Sie gehören zu
einem Vektor, der durch folgendes Dreieck gebildet wird: bedeuten. Sie gehören zu
einem Vektor, der durch folgendes Dreieck gebildet wird:
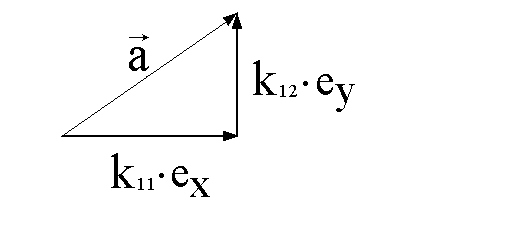 Den Betrag des Vektors
Den Betrag des Vektors 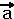 kann man nun ganz leicht mit dem Satz
des Pythagoras berechnen: kann man nun ganz leicht mit dem Satz
des Pythagoras berechnen:
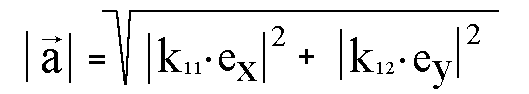 Nun vereinfachen wir: Der Vektor k11·ex hat den Betrag k11, den
der Vektor ex ist ein Einheitsvektor, und Einheitsvektoren haben
den Betrag 1. Ebenso vereinfacht sich k12·ey zu k12
Wir erhalten somit:
Nun vereinfachen wir: Der Vektor k11·ex hat den Betrag k11, den
der Vektor ex ist ein Einheitsvektor, und Einheitsvektoren haben
den Betrag 1. Ebenso vereinfacht sich k12·ey zu k12
Wir erhalten somit:
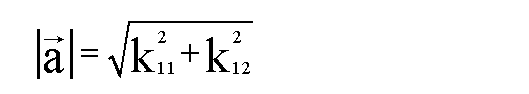 Dies ist aber die gewünschte Formel.
Dies ist aber die gewünschte Formel.
|