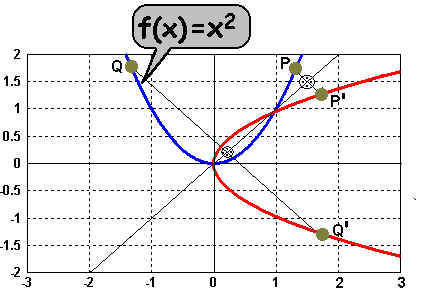
Nun wollen wir die Potenzfunktion f(x)=x² (blau) umkehren. Dazu
spiegeln wir alle Punkte der Funktion an der Winkelhalbierenden
des 1.und 3.Quadraten (im Beispiel wird dadurch P zu P' und Q zu Q').
Es entsteht der Graph einer Relation (rot), jedoch keine Funktion:


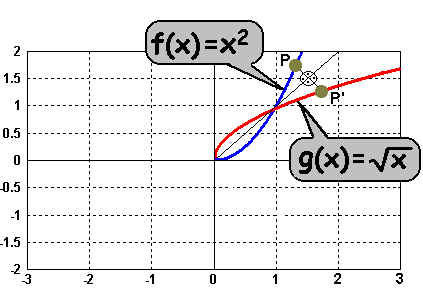
Wenn wir nun aber den Definitionsbereich der Potenzfunktion (blau)
auf die nicht-negativen reellen Zahlen einschränken, dann erhalten
wir eine Umkehrfunktion, und zwar die Quadratwurzelfunktion.

Für die Quadratwurzelfunktion gilt daher:

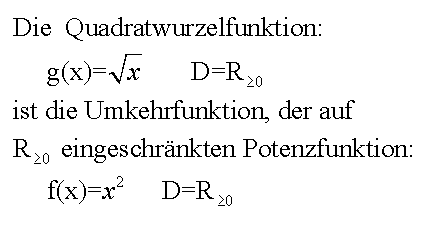
Ebenso gilt für die allgemeine Wurzelfunktion