|
|||
| Beispiel: Wir haben gesagt, daß man Wurzelgleichungen durch Potenzieren löst. Im Bild links lösen wir die Wurzelgleichung und erhalten als Ergebnis 14. |
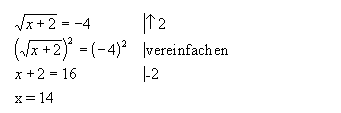 |
||
| Probe
machen: Nun machen wir die Probe, d.h. wir setzen die Lösung (die Zahl 14) in die ursprüngliche Gleichung ein, und überprüfen ob sich eine wahre oder eine falsche Aussage ergibt. Wir stellen fest, daß die Zahl 14 keine Lösung ist. Wie kommt das? |
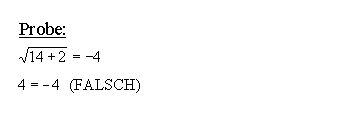 |
||
| Erklärung: Die falsche Lösung entstand, weil wir zum Lösen der Wurzelgleichung die Rechenoperation "Potenzieren" benutzt haben. Das Potenzieren ist aber keine Äquivalenzumformung, denn beim Potenzieren können Scheinlösungen hinzukommen. Weil man zum Lösen von Wurzelgleichungen stets Potenzieren muß, muß man auch immer die Probe machen. |
|||
| Nach dem Lösen einer
Wurzelgleichung muß man immer die Probe machen |