1. Grundintegrale (ausführliche Erklärung des Begriffs im Video des Integrals T200)

Nr.	Integral	Link	Lösungsweg	Angewendete Techniken/Formeln	Anmerkungen
T200		Video	Ergibt sich beim Differenzieren der Tangensfunktion	>
T210		Video folgt	analog zu T200	>

2. Berechnete Integrale: Werden durch Integrationstechniken (Substitution, Partielle Integration usw.)
    aus Grundintegralen und/oder aus zuvor berechneten Integralen gefunden

Nr.	Integral	Link	Lösungsweg	Techniken/Formeln	Anmerkungen
T1000		Video	Rückführung auf Nr. T200 und T210, also auf die zwei Grundintegrale:	> Trigonometrischer Pythagoras
T2000		Video	Substitution: u=sin(x) Man erhält dann eine Potenzfunktion, die man nach der Potenzregel (Grundintegral) integrieren kann	> Substitution > Potenzregel > Ableitung einer Potenz
T2100		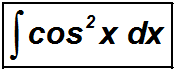Video	Man könnte hier zweimal partiell integrieren. Schneller geht es aber, wenn man nur einmal partiell integriert und dann den trigonometrischen Pythagoras anwendet	> Partielle Integration > Trig. Pythagoras
T3000		Text	1. tan(x)=sin(x)/cos(x) 2. cos(x) substituieren	> Substitution
T4000		Text folgt	analog zu Nr. T3000	> Substitution
T5000		Video	Rückführung auf Nr. T3000 und Nr. T4000	> Trigonometrischer Pythagoras > Bruchrechnung > tan(x)=sin(x)/cos(x) > loga–logb=log(a/b)
T6000		Video	Rückführung auf Nr. T5000	> Substitution x=2u > Formel für doppelten Winkel:    sin(2a)=2·sin(a)·cos(a)
T7000		Video	Lösung durch normale Substitution u=sinx mit einer (recht einfachen) Partialbruchzerlegung	> Normale Substitution > Partialbruchzerlegung > Fast alle trig. Formeln
	Alternative Methode	Video	Lösung durch die Weierstrass Substitution u=tan(x/2) und die Weierstrass Umrechnungsformeln	> Weierstrass Substitution > Fast alle trig. Formeln
	Alternative Methode	Video	Durch einen Trick: Erweitern mit secx+tanx Herleitung des Tricks erfolgt über das Aufstellen und Lösen einer Differentialgleichung: Video	> Fast alle trig. Formeln
	Alternative Methode	Video folgt	Durch Rückführung auf IntegralT6000 über die Beziehung: cos(x)=sin(x+Pi/2)	>

HGF (Häufig gestellte Fragen zur trig. Integralsammlung):

1. Was bedeutet sin²x ?
 
Der Ausdruck sin²x bedeutet (sin x)². Man schreibt es auf diese Art, damit man es nicht mit  sin x² verwechselt.

2. Warum finde ich Integrale wie z.B. nicht?
 
Weil man den Integranden mit Hilfe der Bruchrechnung in zwei Terme zerlegen kann,
und dann jeden Term einzeln integrieren darf: