Diese Seite ist nur für Kenner der Differentialrechnung (Oberstufe):

Die Funktionswerte von g(x) liegen im Bereich 0<x<1 zwar unterhalb von f(x),
die Steigerung von g(x) wird aber bereits ab einem bestimmten Punkt innerhalb
dieses Intervalls größer als f(x):

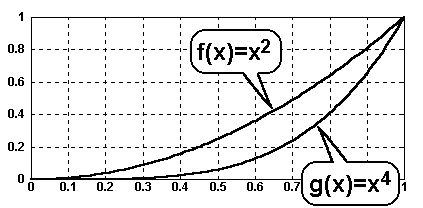
Diesen Punkt, an dem g(x) steiler wird, kann man mit Hilfe der
Differentialrechnung bestimmen. Die Steigungen gleichsetzen:

       f ' (x) = g ' (x)

      (x²) ' =  (x⁴) '

Ableitungen bilden:

      2x= 4x³

Kubische Gleichung durch Ausklammern von x lösen:

     4x³–2x=0
     x(4x²–2)=0            1.Lösung:  0

     4x²–2=0
     4x²=2
     x²=0.5
     x=0.707                 2.Lösung:   0.707

Die Funktion f(x) und g(x) haben also für x=0 und x=0.707
die gleiche Steigung, d.h ab x=0.707 wird g(x) steiler als f(x).
Ab diesem Punkt nähern sich die Funktionswerte von g(x) wieder
den Funktionswerten von f(x), und ab x=1 werden sie dann größer.