Verlauf des Graphen
wenn der Exponent
negativ und gerade
|
 |
Negativer und gerader Exponent |
|
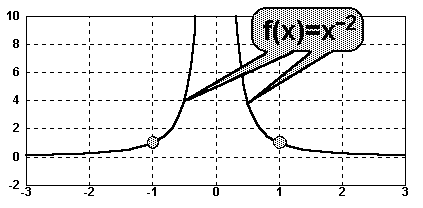
|
 |
Definitionsbereich |
|
Eine Potenzfunktion mit negativen
Exponenten ist für alle reellen Zahlen definiert,
außer für 0, denn x–2=1/x2 , und die Division durch Null ist
ja nicht erlaubt.
Der Definitionsbereich ist also gleich R* oder in der alten Schreibweise:
R\{0}. |
 |
Wertebereich |
|
Weil der Exponent gerade
ist, entstehen nur positive Funktionswerte.
Der Graph verläuft also nur oberhalb der x-Achse. |
 |
Asymptoten und Verhalten in der Nähe von x=0 |
|
Der Graph wächst unbeschränkt
nach oben, wenn die Funktion sich der Stelle
x=0 nähert. Man sagt: Die y-Achse ist eine vertikale (senkrechte) Asymptote.
Für große |x| nähert sich der Graph der x-Achse. Man sagt, die x-Achse ist die
horizontale (waagerechte) Asymptote für große |x|. |
 |
Fixpunkte |
|
Alle Potenzfunktionen mit negativen
und geraden Exponenten verlaufen durch
die Punkte (1/1) und (–1,1) |
 |
Symmetrie |
|
Eine Funktion in der nur gerade
Potenzen von x vorkommen, nennt man gerade Funktion.
Alle geraden Funktionen verlaufen symmetrisch zur y-Achse, und somit auch f(x). |
|