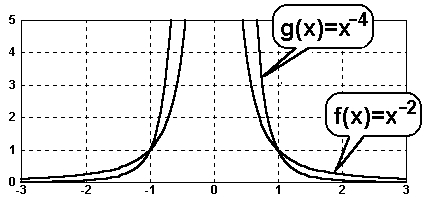
Wie gesagt vergleichen wir hier nur Potenzfunktionen mit negativen und geraden
Exponenten, z.B. f(x)=x^–2 und g(x)=x^–4. Es lassen sich dann folgende Aussagen machen:

Je größer der Exponent einer Potenzfunktion ist:

• ... desto kleiner sind die Funktionswerte im Bereich 0<|x|<1

• ... desto größer sind die Funktionswerte im Bereich |x|>1    

• ... desto flacher ist der Graph in dem Bereich 0<|x|<1

• ... desto steiler nähert sich der Graph der y-Achse (für große x)

Betrachten wir das Intervall x>1 etwas genauer: Wir wissen: In diesem Bereich hat die
Funktion mit dem größeren Exponenten [im Bild f(x)] die größeren Funktionswerte.
Welcher Graph in diesem Intervall aber steiler ist, kann man nicht so einfach sagen.

Zu Beginn des Intervalls ist der Graph von f(x) viel flacher als der Graph von g(x).
Ab einem gewissen Punkt  ist jedoch der Graph von f(x) wieder steiler als der Graph
von  g(x), und die Funktionswerte (Funktionsgraphen) nähern sich wieder einander an.

Dieser Punkt liegt ungefähr bei x=1.41, jedoch müssen wir bis zum Kurs
Differentialrechnung warten, bis wir lernen wie man diesen Punkt berechnen kann.

Analoge Überlegungen kann man auch für das Intervall x<–1 anstellen.

© by www.mathematik.net