Version: Test
©Raddy 2005

Potenzfunktionen II                                          ZURÜCK
Stauchung
in Richtung
der x-Achse
a-absatz.pcx (280 Byte) Satz
Gegeben sei die Potenzfunktion:
    
  f(x)=xn            Beispiel: f(x)=x2
    
Wird das Argument nun mit einer Konstanten k (k>1) multipliziert:
    
  g(x)= (k·x)n      Beispiel: g(x)= (3·x)2
    
dann entsteht ein Graph, der um den Faktor 1/k  in Richtung der
x-Achse gestaucht ist.

              

a-absatz.pcx (280 Byte) Bild und Erklärung 
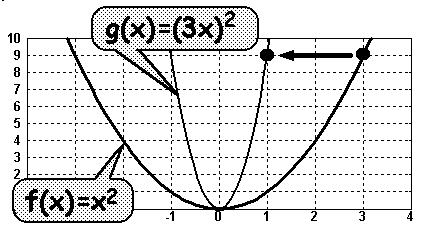
pw1s20p1.pcx (11710 Byte)

Als Beispiel betrachten wir die Funktionen im Bild oben:
    
         f(x) = x2      und     g(x) =  (3x)2

Wird das Argument von f(x) mit den Wert 3 multipliziert,
dann entsteht der Graph von g(x), der dreimal so schnell wächst.
Folglich erreicht die Funktion g(x) einen bestimmten Funktionswert
(im Bild den Funktionswert 9) dreimal so schnell. 
Der Graph von g(x) wirkt dadurch um den Faktor 3
(in Richtung der x-Achse) gestaucht.

Im Bild wurde (als Beispiel) der Punkt (3/9) um den Faktor 3
in Richtung der x-Achse gestaucht, sodaß der Punkt (1/9) entstand.