Nun wollen wir untersuchen, was passiert wenn man an einer Potenzfunktion
mehrere Veränderungen (Verschiebungen, Streckungen usw.) gleichzeitig
vornimmt. So eine Funktion hat die Form:

           g(x)=a(x+b)²+c

Dabei muß man die Veränderungen in der Reihenfolge betrachten, die durch
die Priorität der Rechenoperationen vorgegeben ist, also erst die  Klammer
(Verschiebung rechts/links), dann die Multiplikation (Streckung/Stauchung/Spiegelung)
und zuletzt die Addition (Verschiebung oben/unten).

Als Beispiel untersuchen wir die Funktion:

           g(x)=3(x–1)²+4

1. Die Subtraktion der Zahl 1 vom Argument (x) bewirkt eine Verschiebung
    der Graphen nach rechts, und zwar um den Wert 1.
2. Die Multiplikation mit der Zahl 3 bewirkt ein Streckung in y-Richtung
    um den Faktor 3.
3. Die Addition der Zahl 4 bewirkt ein Verschiebung nach oben um den Wert 4.


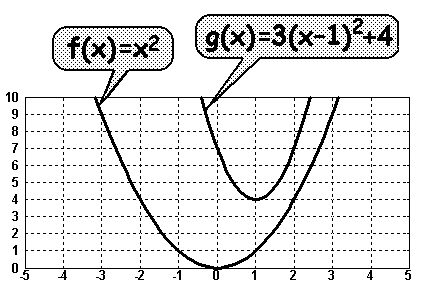
Man nennt diese Form die Scheitelform (Verschiebeform) einer
quadratischen Funktion, weil man die Verschiebung jeden Punktes, und
somit auch des Scheitelpunktes (hier: 1/4), an der Funktion ablesen kann.
Wir werden im Kurs "Quadratische Funktionen" näher darauf eingehen.