Den Graphen einer Potenzfunktion mit rationalen Exponenten
muß nicht wie der Graph einer normalen Potenzfunktion aussehen,
sondern er kann wie der Graph einer Wurzelfunktion aussehen,
und zwar genau dann, wenn der Exponent zwischen 0 und 1 liegt.

Als Beispiel nehmen wir die Funktion:

Wir setzen verschiedene Werte für x ein, und berechnen welcher Wert
sich für y ergibt. Die Ergebnisse tragen wir in eine Wertetabelle ein
(dabei beachte man wieder, daß nur die nicht-negativen Zahlen zum
Definitionsbereich einer Wurzel gehören, d.h. wir dürfen nur positive
Zahlen oder die Null in die Variable x einsetzen):

Mit den Daten der Wertetabelle zeichnen wir jetzt den Graphen:

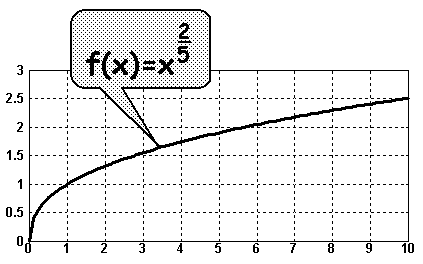
Wir sehen: Der Graph einer "Potenzfunktion mit rationalen
Exponenten" kann wie eine Wurzelfunktion aussehen.