Den Graphen einer Potenzfunktion
mit rationalen Exponenten
kann man auf die übliche Weise herleiten: Man setzt für die
unabhängige Variable x verschiedene Werte ein, und berechnet
die Werte, die sich für die (von x) abhängige Variable y ergeben.
Als Beispiel nehmen wir die Funktion:
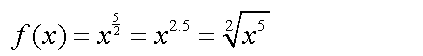
Wir setzen verschiedene Werte für x
ein, und berechnen welcher Wert
sich für f(x) ergibt. Die Ergebnisse tragen wir in eine Wertetabelle ein:
| x |
0 |
0.25 |
0.5 |
0.75 |
1 |
1.25 |
1.5 |
1.75 |
2 |
y=f(x) |
0 |
0.03 |
0.18 |
0.49 |
1 |
1.75 |
2.76 |
4.05 |
5.66 |
Dabei haben wir nur nicht-negative
Zahlen für x gewählt, denn der
Definitionsbereich einer Wurzel besteht ja nur aus nicht-negativen Zahlen.
Mit den Daten der Wertetabelle zeichnen wir jetzt den Graphen:
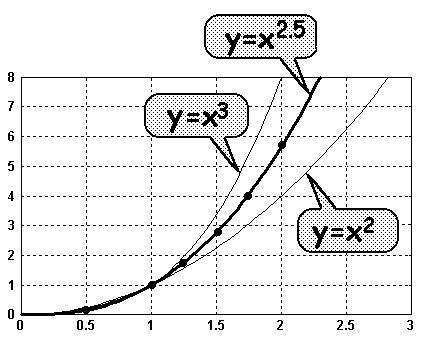
Wir sehen nun 2 Dinge:
1.Der Graph der Potenzfunktion mit rationalen Exponenten größer 1
sieht wie der Graph einer normalen Potenzfunktion aus, jedoch
fehlt ihm der negative Teil, wegen dem oben erwähnten eingeschränkten
Definitionsbereich (Wurzeln sind nur für positive Radikanten definiert).
2.Der Graph der Potenzfunktion mit dem Exponenten 2.5 liegt
zwischen den Potenzfunktionen mit dem Exponenten 2 und 3. |