Definitionsbereich:
Wenn der Exponent positiv und rational ist, dann kann man ihn als Wurzel
schreiben. Da Wurzeln aber nur für nicht-negative Radikanten definiert sind,
besteht der Definitionsbereich nur aus den nicht-negativen Zahlen, d.h. aus
positiven Zahlen und der Null. Das Bild zeigt zwei Beispiele für diesen Fall:



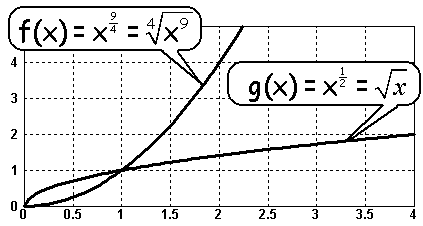
Der Wertebereich
Der Wertebereich umfaßt ebenfalls nur die nicht-negativen Zahlen, d.h.
positive Zahlen und die Null, was man am anschaulich am Graphen erkennt.

Monotonie:
Bei positiven und rationalen Exponenten ist die Potenzfunktion
streng monoton steigend, was man am Graphen erkennt

  

Definitionsbereich:
Wenn der Exponent negativ und rational ist, dann kann man ihn als Wurzel
schreiben, wobei der Radikant ein Bruch ist (wegen dem Minuszeichen).

Da Wurzeln nur für negative Radikanten nicht definiert sind,
gehören die negativen Zahlen nicht zum Definitionsbereich.

Zweitens darf der Nenner nicht Null werden (durch 0 darf man nicht teilen),
und somit gehört auch die Null nicht zum Definitionsbereich.

Somit besteht der Definitionsbereich nur aus positiven Zahlen.



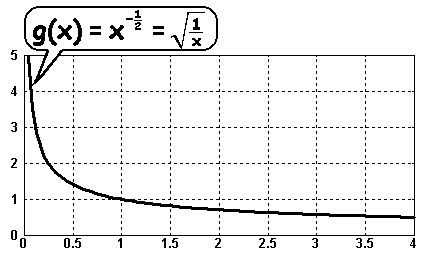
Der Wertebereich
Der Wertebereich umfaßt ebenfalls nur positive Zahlen,
was man am anschaulich am Graphen erkennen kann. 

Monotonie:
Bei negativen rationalen Exponenten ist die Potenzfunktion streng monoton fallend